
甲、乙、丙3人投篮,投进的概率分别是![]()
(I)现3人各投篮1次,求3人都没有投进的概率;
(II)用![]() 表示投篮3次的进球数,求随机变量
表示投篮3次的进球数,求随机变量![]() 的概率分布及数学期望E
的概率分布及数学期望E![]()
解:(Ⅰ)记“甲投篮1次投进”为事件A1,“乙投篮1次投进”为事件A2,“丙投篮1次投进”为事件A3,“3人都没有投进”为事件A. 则 P(A1)=![]() ,P(A2)=
,P(A2)=![]() ,P(A3)=
,P(A3)=![]() .
.
∴ P(A)=P(![]() )=P(
)=P(![]() )?P(
)?P(![]() )?P(
)?P(![]() )
)
=[1-P(A1)]?[1-P(A2)]?[1-P(A3)]
=(1-![]() )(1-
)(1-![]() )(1-
)(1-![]() )=
)=![]() ,
,
∴3人都没有投进的概率为![]() .
.
(Ⅱ)解法一: 随机变量ξ的可能值有0,1,2,3。 则ξ~B(3,![]() ),
),
P(ξ=k)=C3(![]() )k(
)k(![]() )3-k (k=0,1,2,3),Eξ=np=3×
)3-k (k=0,1,2,3),Eξ=np=3×![]() =
=![]() .
.
解法二: ξ的概率分布为
| ξ | 0 | 1 | 2 | 3 |
| P |
|
|
|
|
Eξ=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 2 |
| 5 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年重庆市高三第三次月考考试文科数学 题型:解答题
(13分)甲、乙、丙3人投篮,投进的概率分别是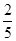 ,
, ,
, .
现3人各投篮1次,
.
现3人各投篮1次,
求:(Ⅰ)3人都投进的概率
(Ⅱ)3人中恰有2人投进的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com