练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，已知梯形ABCD的一底边AB在平面α内，另一底边DC在平面α外，对角线交点O到平面α的距离为D，若AB∶CD=m∶n，求CD到平面α的距离.

    解：∵CD在平面α外，CD∥BA，BAα,

    ∴CD∥平面α.

        作CC1⊥α，C1为垂足，则CC1就是CD和平面α的距离.

        作OO1⊥AC1于O1，∵CC1⊥AC1,∴OO1∥CC1.∵CC1⊥α,∴OO1⊥α.

    ∴OO1是O到平面α的距离，即OO1=D.

        在梯形ABCD中，，∴.

        在平面ACC1内，,∴CC1=.

        因此，CD到平面α的距离为.

    点评:求线面之间的距离，“作、证、算”三步必不可少，即找出代表距离的垂线段并证明之，然后构造平面图形（多数为三角形）来算出.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，已知梯形ABCD中，AD∥BC，∠ABC=90°，AD=a，BC=2a，∠DCB=60°，在平面ABCD内，过C作l⊥CB，以l为轴将梯形ABCD旋转一周，求所得旋转体的表面积及体积．

    查看答案和解析>>

    科目：高中数学 来源：浙江省温州市温州中学2012届高三第三次模拟考试数学试题 题型：044

    如图，已知平面ABC⊥平面BCDE，△DEF与△ABC分别是棱长为1与2的正三角形，AC∥DF，四边形BCDE为直角梯形，DE∥BC，BC⊥CD，CD＝1，点G为△ABC的重心，N为AB中点，＝λ(λ∈R，λ＞0)．

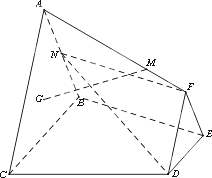
    (Ⅰ)当时，求证：GM∥平面DFN．

    (Ⅱ)若直线MN与CD所成角为，试求二面角M－BC－D的余弦值．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江苏省南京市高三第二次模拟考试数学卷 题型：解答题

    在A、B、C、D四小题中只能选做2题，每小题10，共计20分。请在答题卡指定区域作答。解答应写出文字说明、证明过程或演算步骤。

    A、选修4-1：几何证明选讲

       如图，已知梯形ABCD为圆内接四边形，AD//BC，过C作该圆的切线，交AD的延长线于E，求证：ΔABC∽ΔEDC。

    B、选修4-2：矩形与变换

    已知 为矩阵属于λ的一个特征向量，求实数a，λ的值及A2。

    C、选修4-4：坐标系与参数方程

       在平面直角坐标系xoy中，曲线C的参数方程为（α为参数），曲线D的参数方程为，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。

    D、选修4-5：不等式选讲

       已知a，b都是正实数，且ab=2。求证：（1+2a）（1+b）≥9。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

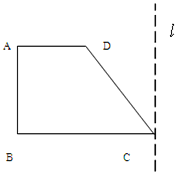    如图，已知梯形ABCD中，AD∥BC，∠ABC=90°，AD=a，BC=2a，∠DCB=60°，在平面ABCD内，过C作l⊥CB，以l为轴将梯形ABCD旋转一周，求所得旋转体的表面积及体积．

    查看答案和解析>>

    科目：高中数学 来源：0110 期末题 题型：解答题

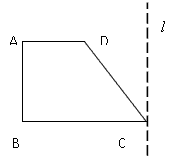
    如图，已知梯形ABCD中，AD∥BC，∠ABC=90°，AD=a，BC=2a，∠DCB=60°，在平面ABCD内，过C作l⊥CB，以l为轴将梯形ABCD旋转一周，求所得旋转体的表面积及体积。

    查看答案和解析>>

    同步练习册答案