练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    证明sin（α+β）sin（α－β）=sin2α－sin2β，并利用该式计算sin220°+     sin80°·sin40°的值．

    证明：sin（α+β）sin（α－β）=（sinαcosβ+cosαsinβ）（sinαcosβ－cosαsinβ）

    =sin2αcos2β－cos2αsin2β

    =sin2α（1－sin2β）－（1－sin2α）sin2β

    =sin2α－sin2αsin2β－sin2β+sin2αsin2β[来源:学。科。网]

    =sin2α－sin2β，

    所以左边=右边，原题得证．

    计算sin220°+sin80°·sin40°，需要先观察角之间的关系．经观察可知80°=60°+    20°，40°=60°－20°，

    所以sin220°+sin80°·sin40°=sin220°+sin（60°+20°）·sin（60°－20°）

    =sin220°+sin260°－sin220°

    =sin260°

    =．

    分析：此题目要灵活运用“化切为弦”的方法，再利用两角和与差的三角函数关系式整理化简．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f（x）=ax3+
    1
    2
    sinθx2-2x+c的图象经过点(1，
    37
    6
    )    ，且在区间（-2，1）上单调递减，在[1，+∞）上单调递增．
    （1）证明sinθ=1；
    （2）求f（x）的解析式；
    （3）若对于任意的x1，x2∈[m，m+3]（m≥0），不等式|f（x1）-f（x2）|≤
    45
    2
    恒成立，试问：这样的m是否存在，若存在，请求出m的范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    ①已知sinα-cosα=
    1
    5
    ，求sin2α的值．
    ②证明
    sin(2α+β)
    sinα
    -2cos(α+β)=
    sinβ
    sinα
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年湖北省黄石市大冶市华中学校高三数学滚动训练（三）（解析版） 题型：解答题

    已知函数f（x）=ax3+sinθx2-2x+c的图象经过点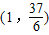，且在区间（-2，1）上单调递减，在[1，+∞）上单调递增．
    （1）证明sinθ=1；
    （2）求f（x）的解析式；
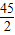    （3）若对于任意的x1，x2∈[m，m+3]（m≥0），不等式|f（x1）-f（x2）|≤恒成立，试问：这样的m是否存在，若存在，请求出m的范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2010年广东省广州109中高考数学模拟试卷（文科）（解析版） 题型：解答题

    已知函数f（x）=ax3+sinθx2-2x+c的图象经过点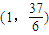，且在区间（-2，1）上单调递减，在[1，+∞）上单调递增．
    （1）证明sinθ=1；
    （2）求f（x）的解析式；
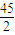    （3）若对于任意的x1，x2∈[m，m+3]（m≥0），不等式|f（x1）-f（x2）|≤恒成立，试问：这样的m是否存在，若存在，请求出m的范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2011年湖北省鄂州市高三摸底数学试卷（文科）（解析版） 题型：解答题

    已知函数f（x）=ax3+sinθx2-2x+c的图象经过点，且在区间（-2，1）上单调递减，在[1，+∞）上单调递增．
    （1）证明sinθ=1；
    （2）求f（x）的解析式；
    （3）若对于任意的x1，x2∈[m，m+3]（m≥0），不等式|f（x1）-f（x2）|≤恒成立，试问：这样的m是否存在，若存在，请求出m的范围；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案