Question

写出下图区域所表示的角的集合.

                  (1)                                      (2)

Answer 1

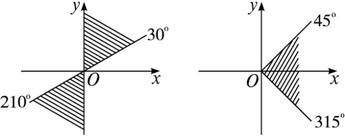
解析:(1)∵k·360°+30°≤α≤k·360°+90°或k·360°+210°≤α≤k·360°+270°,k∈Z,

即2k·180°+30°≤α≤2k·180°+90°或

(2k+1)180°+30°≤α≤(2k+1)180°+90°,k∈Z,

∴n·180°+30°≤α≤n·180°+90°,n∈Z.

∴图(1)区域所表示的角α的集合为

{α|k·180°+30°≤α≤k·180°+90°,k∈Z}.

(2)∵315°角与-45°角的终边相同,

∴k·360°-45°≤β≤k·360°+45°,k∈Z.

∴图(2)区域所表示的角β的集合为

{β|k·360°-45°≤β≤k·360°+45°,k∈Z}.

点评:区间角集合的表示一般有两种情况:(1)分别用正角或负角(零角)终边相同的角的集合表示区域的边界;(2)都用正角(或零角)的终边相同的角的集合表示区域的边界.如本题(2)中就要注意315°角的终边的角的选取,若选315°,且45°角不变,则写出的不等式不成立,写出的集合{β|k·360°+315°≤β≤k·360°+45°,k∈Z}为空集,故应将315°角的终边的角写为-45°(若第一象限的终边写45°,则第四象限只能写-45°).若第四象限的终边写315°,那么第一象限只能写405°.