练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知α，β，γ是不重合平面，a，b是不重合的直线，下列说法正确的是

    [　　]

    A．“若a∥b，a⊥α，则b⊥α”是随机事件

    B．“若a∥b，a?α，则b∥α”是必然事件

    C．“若α⊥γ，β⊥γ，则α⊥β”是必然事件

    D．“若a⊥α，a∩b＝P，则b⊥α”是不可能事件

    答案：D
    解析：


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    现有若干颗形状完全相同的玻璃球，已知其中一颗略重，其余各颗重量均相同，要求
    使用天平（不用砝码）将略重的那颗玻璃球找出来．小龙的方案是：首先任取两颗放在天平的两侧进行称量，若天平不平衡，则重的那边为略重的那颗玻璃球，若天平平衡，则两颗都取下，从剩下的玻璃球中再任取两颗放在天平两侧进行称量，如此进行下去，直到找到那颗略重的玻璃球为止．若小龙恰好在第一次就找出略重的那颗玻璃球的概率为
    27
    ．
    （1）请问共有多少颗玻璃球？
    （2）设ξ为找到略重的那颗玻璃球时已称量的次数，求ξ的分布列与数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•绵阳一模）现有若干枚形状完全相同的硬币，已知其中一枚略重，其余各枚重量均相同，要求使用天平（不用砝码），将略重的那枚硬币找出来．小王的方案是：首先任取两枚放在天平两侧进行称量，若天平不平衡，则重的那边为略重的那枚硬币：若天干平衡，将两枚都取下，从剩下的硬币中再任取两枚放在天平两侧进行称量，如此进行下去，直到找到那枚略重的硬币为止．若小王恰好在第一次就找出略重的那枚硬币的概率为
    29
    ．
    （I ）请问共有多少枚硬币？
    （II）设ξ为找到略重那枚硬币时己称量的次数，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源：2014届甘肃天水一中高二下学期期末考试理科数学试卷（解析版） 题型：选择题

    已 知 A 、 B 、 C 是 平 面 上 不 共 线 的 三 点 ， O 是 三 角形 ABC 的 重 心 ， 动 点 P 满 足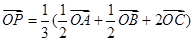，则点 P 一定为三角形的 （   ）

    （A）AB 边中线的中点

    （B）AB 边中线的三等分点（非重心）

    （C）重心

    （D）AB边的中点

     

    查看答案和解析>>

    科目：高中数学 来源：2014届黑龙江省高二下学期期末考试理科数学试卷（解析版） 题型：解答题

    已知某池塘养殖着鲤鱼和鲫鱼，为了估计这两种鱼的数量，养殖者从池塘中捕出两种鱼各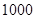只，给每只鱼做上不影响其存活的标记，然后放回池塘，待完全混合后，再每次从池塘中随机的捕出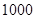只鱼，记录下其中有记号的鱼的数目，立即放回池塘中。这样的记录做了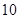次，并将记录获取的数据做成以下的茎叶图。

    （Ⅰ）根据茎叶图计算有记号的鲤鱼和鲫鱼数目的平均数，并估计池塘中的鲤鱼和鲫鱼的数量；

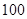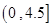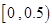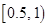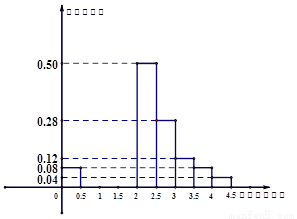
    （Ⅱ）为了估计池塘中鱼的总重量，现从中按照（Ⅰ）的比例对条鱼进行称重，据称重鱼的重量介于（单位：千克）之间，将测量结果按如下方式分成九组：第一组、第二组；……，第九组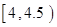。右图是按上述分组方法得到的频率分布直方图的一部分。

    ①估计池塘中鱼的重量在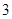千克以上（含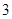千克）的条数；

    ②若第二组、第三组、第四组鱼的条数依次成公差为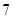的等差数列，请将频率分布直方图补充完整；

    ③在②的条件下估计池塘中鱼的重量的众数、中位数及估计池塘中鱼的总重量；

    （Ⅲ）假设随机地从池塘逐只有放回的捕出只鱼中出现鲤鱼的次数为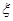，求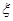的数学期望。

     

    查看答案和解析>>

    科目：高中数学 来源：2012年四川省绵阳市高考数学一模试卷（理科）（解析版） 题型：解答题

    现有若干枚形状完全相同的硬币，已知其中一枚略重，其余各枚重量均相同，要求使用天平（不用砝码），将略重的那枚硬币找出来．小王的方案是：首先任取两枚放在天平两侧进行称量，若天平不平衡，则重的那边为略重的那枚硬币：若天干平衡，将两枚都取下，从剩下的硬币中再任取两枚放在天平两侧进行称量，如此进行下去，直到找到那枚略重的硬币为止．若小王恰好在第一次就找出略重的那枚硬币的概率为．
    （I ）请问共有多少枚硬币？
    （II）设ξ为找到略重那枚硬币时己称量的次数，求ξ的分布列和数学期望．

    查看答案和解析>>

    同步练习册答案