
如图所示,已知一直线
a分别与两平行直线b,c相交,求证:
a,b,c三线共面.
|
证法 1:∵b∥c,则b,c确定一个平面,设为α,如上图所示.令  , ,
∴  ,即直线 ,即直线 , ,
∴ a,b,c三线共面.证法 2:∵a与b是相交直线,则a,b确定一个平面,设为a,如图.
设  ,过A点在α内作直线 ,过A点在α内作直线 , ,
∵  . .
又∵ c与 相交于点A,c与 相交于点A,c与 重合, 重合,
∴ a,b,c三线共面.证法 3:∵b∥c,∴b,c确定一个平面,设为α.又∵ a、b是相交直线,∴a、b确定一个平面,设为β.设  ,则 ,则 , ,
∴点 A和直线b既在平面α内,又在平面β内,且 , ,
∴平面 α与平面β重合.∴ a、b、c三线共面. |
|
思路1:两条平行直线b,c确定一个平面,再证a也在这个平面内. 思路2:两条相交直线a,b确定一个平面,再证c也在这个平面内. 思路3:由推论2和3知,相交直线a,b确定一个平面,平行直线b,c也确定一个平面,只需证明上述两个平面重合即可. |


科目:高中数学 来源: 题型:
 如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆
如图所示,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆| x2 |
| 2 |
| 4 |
| 3 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
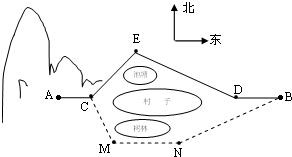 某村子的正西是一片山区.山脚下A处已建一处采石场,村子的北边有一池塘,南边有一树林,在B处是个石粉厂,在采石场采到的石料由公路ACEDB运输到石粉厂,如图所示.已知A,C,D,B在一条直线上,AC=2km,CE=2km,ED=3km,DB=2km,∠CED=120°.
某村子的正西是一片山区.山脚下A处已建一处采石场,村子的北边有一池塘,南边有一树林,在B处是个石粉厂,在采石场采到的石料由公路ACEDB运输到石粉厂,如图所示.已知A,C,D,B在一条直线上,AC=2km,CE=2km,ED=3km,DB=2km,∠CED=120°.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(2006•石景山区一模)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足| AM |
| AP |
| NP |
| AM |
| FG |
| FH |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com