练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题14分）、已知函数

    （1）若函数的最小值是，且对称轴是， 

    求的值：

    （2）在（1）条件下求在区间的最小值w.w.

    （1）       

      

    （2）当时，即时 

    在区间上单调递减

    当时，即时 

    在区间上单调递减，在区间上单调递增   

    当时， 在区间上单调递增，

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （本题满分14分）

    ．
     
        已知：（）是方程的两根，且，.

          （1）求的值；             

    （2）设，求证：；

          （3）求证：对有 w。.w.．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省龙岩市高三上学期期末考试数学理卷（一级学校） 题型：解答题

    （本题满分14分）

    　   已知函数.

    　　（Ⅰ）若为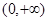上的单调函数，试确定实数的取值范围;[来源:学_科_网Z_X_X_K]

    　　（Ⅱ）求函数在定义域上的极值；

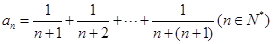    （Ⅲ）设,求证：.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省龙岩市高三第一次教学质量检测一级达标校数学理卷 题型：解答题

    （本题满分14分）

    　   已知函数.

    　　（Ⅰ）若为上的单调函数，试确定实数的取值范围;

    　　（Ⅱ）求函数在定义域上的极值；

    （Ⅲ）设,求证：.

     

    查看答案和解析>>

    科目：高中数学 来源：2013届上海市高二年级期终考试数学 题型：解答题

    （本题满分14分）

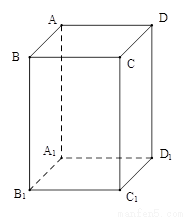
    (文科)已知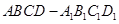是底面边长为1的正四棱柱，高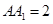.求：

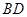    ⑵   异面直线与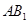所成的角的大小（结果用反三角函数表示）；

    ⑵ 四面体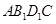的体积.

     

     

     

     

     

     

    查看答案和解析>>

    同步练习册答案