
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证数列![]() 中不存在任意三项按原来顺序成等差数列;
中不存在任意三项按原来顺序成等差数列;
(3)若从数列![]() 中依次抽取一个无限多项的等比数列,使它的所有项和
中依次抽取一个无限多项的等比数列,使它的所有项和![]() 满足
满足![]() ,这样的等比数列有多少个?
,这样的等比数列有多少个?
解:(1)当![]() 时,
时,![]() ,则
,则![]() .
.
又![]() ,
,![]() ,两式相减得
,两式相减得![]() ,
,
![]() 是首项为1,公比为
是首项为1,公比为![]() 的等比数列,
的等比数列,
![]() --------------------------------------------------------4分
--------------------------------------------------------4分
(2)反证法:假设存在三项按原来顺序成等差数列,记为![]()
则![]() ,
,
![]() (*) 又
(*) 又![]()
![]()
![]() *式左边是偶数,右边是奇数,等式不成立
*式左边是偶数,右边是奇数,等式不成立
![]() 假设不成立 原命题得证. ------------------------------------------------8分
假设不成立 原命题得证. ------------------------------------------------8分
(3)设抽取的等比数列首项为![]() ,公比为
,公比为![]() ,项数为
,项数为![]() ,
,
且满足![]() ,
,
则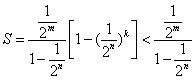 又
又![]()
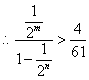 整理得:
整理得:![]() ①
①
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 将
将![]() 代入①式整理得
代入①式整理得![]()
![]()
经验证得![]() 不满足题意,
不满足题意,![]() 满足题意.
满足题意.
综上可得满足题意的等比数列有两个. -------------------------------------16分


科目:高中数学 来源:2011届福建省龙岩市高三上学期期末考试数学理卷(非一级校) 题型:解答题
(本题满分13分)
已知数列 的前
的前 项和为
项和为 ,满足
,满足 .
.
(Ⅰ)证明:数列 为等比数列,并
为等比数列,并 求出
求出 ;
;
(Ⅱ)设 ,求
,求 的最大项.
的最大项.
查看答案和解析>>
科目:高中数学 来源:2011年四川省泸县二中高2013届春期重点班第一学月考试数学试题 题型:解答题
(本小题14分)已知数列{ }的前
}的前 项和为
项和为 ,且
,且 =
= (
( );
); =3
=3
且 (
( ),
),
(1)写出


 ;
;
(2)求数列{ },{
},{ }的通项公式
}的通项公式 和
和 ;
;
(3)设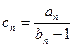 ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2015届广东省高一下学期期中数学试卷(解析版) 题型:解答题
已知数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令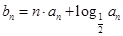 ,数列
,数列 的前
的前 项和为
项和为 ,若不等式
,若不等式 对任意
对任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com