练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知有一列数1-+-++…+-，设计算法求这个数列前100项和，并画出程序框图.

    解:由于项数之间的递增是连续的，且第一项为1，所以循环变量可设为k，k初始值为0且k的变化方式为k=k+1.

    第二步来设计循环体部分：循环体是个累加的过程，将1,2,3,…变为1,-,,-,…,并且把它们一次次的加起来，可以用赋值语句S=S+(-1)k-1来起到这个效果.

    最后我们来设计循环终止条件，我们知道这个循环需要运行100次，当k＞100时我们就退出循环结构.则设置循环终止条件为k＞100.这个地方注意是否写在正确位置.程序框图如图1-1-22所示.

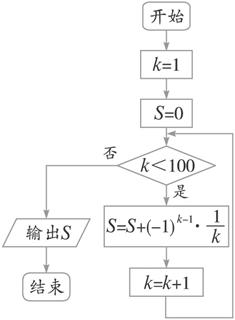
    图1-1-22

    思路分析：这列数相邻的两项符号不同，且第一项为正，第二项为负，依次下去.我们可以通过(-1)k-1来调整这个符号.再就是可以看出每一项为连续的自然数的倒数.这样我们可以设计循环结构来解决.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    一学生参加某高校的自主招生考试，须依次参加A、B、C、D、E五项考试，如果前四项中有两项不合格或第五项不合格，则该考生就被淘汰，考试即结束；考生未被淘汰时，一定继续参加后面的考试．已知每一项测试都是相互独立的，该生参加A、B、C、D四项考试不合格的概率均为
    1
    3
    ，参加第五项不合格的概率为
    1
    4
    ．
    （1）求该生被录取的概率．
    （2）记该生参加考试的项数为ξ，求ξ的分布列和期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知有一列数
    1
    2
    ，
    2
    3
    ，
    3
    4
    ，…，
    n
    n+1
    ，设计框图实现求该列数前20项的和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    “雪花曲线”因其形状类似雪花而得名，它可以以下列方式产生，如图，有一列曲线P1，P2，P3…，，已知P1是边长为1的等边三角形，Pn+1是对Pn进行如下操作得到：将Pn的每条边三等分，以每边中间部分的线段为边，向外作等边三角形，再将中间部分的线段去掉（n=1，2，3…）．
    （1）记曲线P1n的边长和边数分别为an和bn（n=，1，2，…），求an和bn的表达式；
    （2）记Sn为曲线Pn所围成图形的面积，写出Sn与Sn-1的递推关系式，并求Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知有一列数1-+-++…+,设计算法求这个数列前100项的和.

    查看答案和解析>>

    同步练习册答案