函数的图像和函数的图像的交点个数为 . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

函数的图像和函数的图像的交点个数为

。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

（08年安徽信息交流）（本题满分12分）

已知函数的图象在y轴上的截距为，相邻的两个最值点是和

（1）求函数；

（2）设，问将函数的图像经过怎样的变换可以得到的图像？

（3）画出函数在区间上的简图．

查看答案和解析>>

科目：高中数学 来源： 题型：

17.本题满分10分已知函数的图象在y轴上的截距为，相邻的两个最值点是和（1）求函数；（2）设，问将函数的图像经过怎样的变换可以得到的图像？（3）画出函数在区间上的简图．

查看答案和解析>>

科目：高中数学 来源：2012-2013学年安徽省高三第一次月考理科数学试卷（解析版） 题型：填空题

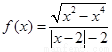函数.给出函数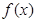下列性质：⑴函数的定义域和值域均为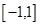；⑵函数的图像关于原点成中心对称；⑶函数在定义域上单调递增；⑷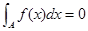（其中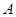为函数的定义域）；⑸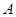、为函数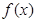图象上任意不同两点，则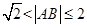.请写出所有关于函数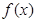性质正确描述的序号 .

查看答案和解析>>

科目：高中数学 来源：2012届湖北省黄石市高二数学上学期期末考试 题型：选择题

经济学中的“蛛网理论”（如下图），假定某种商品的“需求—价格”函数的图像为直线，“供给—价格”函数的图像为直线，它们的斜率分别为，与的交点为“供给—需求”平衡点，在供求两种力量的相互作用下，该商品的价格和产销量，沿平行于坐标轴的“蛛网”路径，箭头所指方向发展变化，最终能否达于均衡点，与直线、的斜率满足的条件有关，从下列三个图中可知最终能达于均衡点的条件为 ( )