
如图所示,矩形ABCD和梯形BEFC所在平面互相垂直,
BE∥CF,∠BCF=∠CEF=90°,AD=![]() ,EF=2.
,EF=2.
(1)求证:AE∥平面DCF;
(2)当AB的长为何值时,二面角A—EF—C的大小为60°?

(1)证明略 (2) 当AB为![]() 时,二面角A—EF—C的大小为60°
时,二面角A—EF—C的大小为60°
方法一 (1) 过点E作EG⊥CF交CF于G,
连接DG.可得四边形BCGE为矩形,
又四边形ABCD为矩形,
![]() 所以AD EG,从而四边形ADGE为平行四边形,
所以AD EG,从而四边形ADGE为平行四边形,
故AE∥DG.
因为AE![]() 平面DCF,DG
平面DCF,DG![]() 平面DCF,
平面DCF,
所以AE∥平面DCF.
(2) 过点B作BH⊥EF交FE的延长线于H,连接AH.
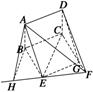 由平面ABCD⊥平面BEFC,AB⊥BC,
由平面ABCD⊥平面BEFC,AB⊥BC,
得AB⊥平面BEFC,
从而AH⊥EF,所以∠AHB为二面角A—EF—C的平面角.
在Rt△EFG中,因为EG=AD=![]() ,EF=2,
,EF=2,
所以∠CFE=60°,FG=1,
又因为CE⊥EF,所以CF=4,
从而BE=CG=3.
于是BH=BE·sin∠BEH=![]() .
.
因为AB=BH·tan∠AHB=![]() ×
×![]() =
=![]() ,
,
所以当AB为![]() 时,二面角A—EF—C的大小为60°.
时,二面角A—EF—C的大小为60°.
方法二 如图所示,以点C为坐标原点,以CB、CF和CD所在直线分别作为x轴、y轴和z轴,建立空间直角坐标系C—xyz.
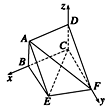
设AB=a,BE=b,CF=c,
则C(0,0,0),A(![]() ,0,a),
,0,a),
B(![]() ,0,0),E(
,0,0),E(![]() ,b,0),F(0,c,0).
,b,0),F(0,c,0).
(1)![]() =(0,b,-a),
=(0,b,-a),![]() =(
=(![]() ,0,0),
,0,0),![]() =(0,b,0),
=(0,b,0),
所以![]() ·
·![]() =0,
=0,![]() ·
·![]() =0,从而CB⊥AE,CB⊥BE.
=0,从而CB⊥AE,CB⊥BE.
AE∩BE=E,所以CB⊥平面ABE.
因为CB⊥平面DCF,
所以平面ABE∥平面DCF,AE![]() 平面ABE.
平面ABE.
故AE∥平面DCF.
(2)因为![]() =(-
=(-![]() ,c-b,0),
,c-b,0),![]() =(
=(![]() ,b,0).
,b,0).
![]() ·
·![]() =0,|
=0,|![]() |=2,
|=2,
所以![]() 解得
解得![]()
所以E(![]() ,3,0),F(0,4,0).
,3,0),F(0,4,0).
设n=(1,y,z)与平面AEF垂直,
则n·![]() =0,n·
=0,n·![]() =0,解得n=(1,
=0,解得n=(1,![]() ,
,![]() ).
).
又因为BA⊥平面BEFC,![]() =(0,0,a),
=(0,0,a),
所以|cos〈n, ![]() 〉|=
〉|=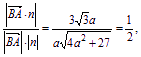
解得a=![]() .
.
所以当AB为![]() 时,二面角A—EF—C的大小为60°.
时,二面角A—EF—C的大小为60°.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
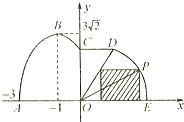 如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y=Asin(ωx+φ)(A>0,ω>0,| π |
| 2 |
| 2 |
| 3 |
 |
| DE |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,在△ABC中,AC=1,AB=3,∠ACB=
如图所示,在△ABC中,AC=1,AB=3,∠ACB=| π | 2 |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省南京市金陵中学高考数学预测试卷(2)(解析版) 题型:解答题
 <φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3
<φ<π),x∈[-3,0]的图象,且图象的最高点为B(-1,3 );赛道的中间部分为
);赛道的中间部分为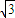 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三预测卷2数学 题型:解答题
(本小题满分14分)
如图,某市拟在道路的一侧修建一条运动赛道,赛道的前一部分为曲线段ABC,该曲线段为函数y= (A>0,
(A>0, >0,
>0, <
< <
< ),x∈[-3,0]的图象,且图象的最高点为B(-1,
),x∈[-3,0]的图象,且图象的最高点为B(-1, );赛道的中间部分为
);赛道的中间部分为 千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧
千米的水平跑到CD;赛道的后一部分为以O圆心的一段圆弧 .
.

(1)求 ,
, 的值和∠DOE的值;
的值和∠DOE的值;
(2)若要在圆弧赛道所对应的扇形区域内建一个“矩形草坪”,如图所示,矩形的一边在道路AE上,一个顶点在扇形半径OD上.记∠POE= ,求当“矩形草坪”的面积最大时
,求当“矩形草坪”的面积最大时 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com