(1)证明:取y=1,则f(x+1)+1=f(x)+f(1)=f(x).设x
1,x
2∈R,且x
1>x
2,则x
1-x
2>0,x
1-x
2+1>1,
因为当x>1时f(x)<0,所以f(x
1-x
2+1)<0.
f(x
1)=f(x
1+1)+1=f[x
2+(x
1-x
2+1)]+1
=f(x
2)+f(x
1-x
2+1)-1+1=f(x
2)+f(x
1-x
2+1).
因为f(x
1-x
2+1)<0,所以f(x
2)<f(x
1).
所以函数f(x)在R上是减函数;
(2)解:取x=y=0,得f(0)+1=f(0)+f(0),
所以f(0)=1,
由

,得
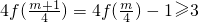
.
所以
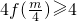
,
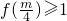
.
因为f(x)为实数集上的减函数,且f(0)=1
所以
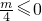
.
则m≤0.
所以实数m的范围是(-∞,0].
分析:(1)通过取y=1,由已知的等式得到f(x)=f(x+1)+1,设x
1,x
2∈R,规定大小后通过转化得到:若x
1>x
2,则所以f(x
1-x
2+1)<0,然后得到f(x
1)=f(x
1+1)+1=f[x
2+(x
1-x
2+1)]+1,展开后分析即可得到答案;
(2)运用f(x)=f(x+1)+1把

的左边展开,然后求出f(0)=1,借助于函数是减函数脱去“f”后求解不等式及可.
点评:本题考查了抽象函数及其应用,考查了特值法判断函数的单调性,考查了学生灵活处理和解决问题的能力,训练了利用函数单调性求解不等式,是中档题.

 ,求实数m的范围.
,求实数m的范围. ,得
,得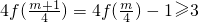 .
.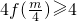 ,
,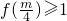 .
.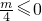 .
. 的左边展开,然后求出f(0)=1,借助于函数是减函数脱去“f”后求解不等式及可.
的左边展开,然后求出f(0)=1,借助于函数是减函数脱去“f”后求解不等式及可.
