
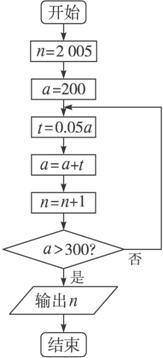
算法分析:先写出解决本例的算法步骤:
第一步,输入2005年的年生产总值.
第二步,计算下一年的年生产总值.
第三步,判断所得的结果是否大于300,若是,则输出该年的年份,算法结束;否则,返回第二步.
由于“第二步”是重复操作的步骤,所以本例可以用循环结构来实现.我们按照“确定循环体”“初始化变量”“设定循环控制条件”的顺序来构造循环结构.
(1)确定循环体:设a为某年的年生产总值,t为年生产总值的年增长量,n为年份,则循环体为t=0.05a,a=a+t,n=n+1.
(2)初始化变量:若将2005年的年生产总值看成计算的起始点,则n的初始值为2005,a的初始值为200.
(3)设定循环控制条件:当“年生产总值超过300万元”时终止循环,所以可通过判断“a>300”是否成立来控制循环.
程序框图如下:


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
| 1 | 5 |
查看答案和解析>>
科目:高中数学 来源:2011届湖南省浏阳一中高三第一次月考文科数学试卷 题型:解答题
(满分13分)
某厂准备投资100万生产A,B两种新产品,据测算,投产后的年收益,A产品是总投入的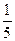 ,B产品则是总投入开平方
,B产品则是总投入开平方 后的2倍.问应该怎样分配投入数,使两种产品的年总收益最大?
后的2倍.问应该怎样分配投入数,使两种产品的年总收益最大?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市微山二中高三(上)期中数学试卷(解析版) 题型:解答题
 ,B产品则是投入数开平方后的2倍,设投入B产品的数为x2(0<x≤10)万元.
,B产品则是投入数开平方后的2倍,设投入B产品的数为x2(0<x≤10)万元.查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省高三第一次月考文科数学试卷 题型:解答题
(满分13分)
某厂准备投资100万生产A,B两种新产品,据测算,投产后的年收益,A产品是总投入的 ,B产品则是总投入开平方后的2倍.问应该怎样分配投入数,使两种产品的年总收益最大?
,B产品则是总投入开平方后的2倍.问应该怎样分配投入数,使两种产品的年总收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com