
分析 问题转化为$\frac{1}{lna}$<lnx+$\frac{4}{lnx}$,x∈(1,100),令h(x)=lnx+$\frac{4}{lnx}$,x∈(1,100),求出h(x)的值域,从而求出a的范围即可.
解答 解:∵$\frac{lo{g}_{a}x}{lnx}$-$\frac{4}{lnx}$<lnx,
∴$\frac{1}{lna}$<lnx+$\frac{4}{lnx}$,x∈(1,100),
令h(x)=lnx+$\frac{4}{lnx}$,x∈(1,100),
则lnx>0,
故h(x)≥2$\sqrt{lnx•\frac{4}{lnx}}$=4,
当且仅当lnx=2时“=”成立,
而h(100)=2ln10+$\frac{2}{ln10}$,
而x→1时,lnx→0,h(x)→+∞,
故h(x)∈[4,+∞),
故$\frac{1}{lna}$<4,
0<a<1时,lna<0,成立,
a>1时,lna>0,
只需lna>$\frac{1}{4}$,即a>${e}^{\frac{1}{4}}$即可,
综上:a∈(0,1)∪(${e}^{\frac{1}{4}}$,+∞),
故答案为:(0,1)∪(${e}^{\frac{1}{4}}$,+∞).
点评 本题考查了函数的单调性、最值问题,考查不等式的性质,是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $y=cos({\frac{3π}{2}-2x})$ | B. | y=|cosx| | C. | $y=sin({\frac{π}{2}+2x})$ | D. | y=|sinx| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3条 | B. | 2条 | C. | 1条 | D. | 0条 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
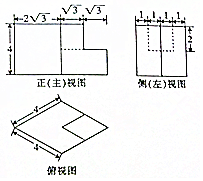
| A. | 64+18$\sqrt{3}$ | B. | 64+16$\sqrt{3}$ | C. | 96 | D. | 92-2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(6)<f(-7)<f(\frac{11}{2})$ | B. | $f(6)<f(\frac{11}{2})<f(-7)$ | C. | $f(-7)<f(\frac{11}{2})<f(6)$ | D. | $f(\frac{11}{2})<f(-7)<f(6)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com