
已知正方形ABCD,ABEF的边长都是1,而且平面ABCD与平面ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<![]() ).
).
(1)求MN的长;
(2)a为何值时,MN的长最小.
|
解:(1)∵面ABCD⊥平面ABEF,面ABCD∩平面ABEF=AB,AB⊥BE,∴BE⊥面ABC.∴AB,BC,BE两两垂直. ∴以B为原点,以BA,BE,BC所在直线为x轴,y轴和z轴,建立如图所求的空间直角坐标系.
则A(1,0,0),B(0,0,0),F(1,1,0),C(0,0,1). 由点N向AB作垂线,设垂足为G,由于 ∴GN= 同理可求得M点的坐标为( (1)由空间两点的距离公式,得MN= (2)由(1)知,MN= ∴当a= 深化升华:通过建立恰当的空间直角坐标系,把空间问题代数化,从而利用二次函数配方法求最值. |
|
本题为2002年高考题的前二问,对该题的求解方法很多,但利用坐标法求解,应该说是既简捷,又易行的方法,通过几种方法的对照比较,体现坐标法解题的优越性. |


 培优口算题卡系列答案
培优口算题卡系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
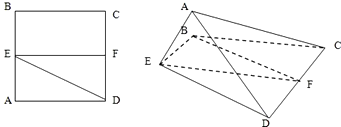 已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).
已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).查看答案和解析>>
科目:高中数学 来源: 题型:
 (2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,
(2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com