
设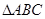 的三边分别为
的三边分别为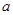 ,
, ,
,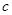 ,
,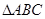 面积为S ,内切圆半径为
面积为S ,内切圆半径为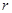 ,则
,则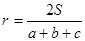 ,类比这个结论可知:四面体
,类比这个结论可知:四面体 的四个面面积分别为
的四个面面积分别为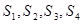 ,内切球半径为
,内切球半径为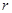 ,四面体
,四面体 的体积为
的体积为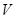 ,则
,则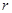 =( )
=( )
A. | B.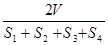 |
C.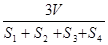 | D.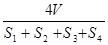 |
C
解析考点:类比推理.
分析:根据平面与空间之间的类比推理,由点类比点或直线,由直线 类比 直线或平面,由内切圆类比内切球,由平面图形面积类比立体图形的体积,结合求三角形的面积的方法类比求四面体的体积即可.
解答: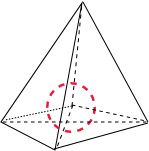
解:设四面体的内切球的球心为O,
则球心O到四个面的距离都是R,
所以四面体的体积等于以O为顶点,
分别以四个面为底面的4个三棱锥体积的和.
则四面体的体积为 V四面体A-BCD=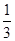 (S1+S2+S1+S4)R
(S1+S2+S1+S4)R
∴R=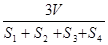
故选C.
点评:类比推理是指依据两类数学对象的相似性,将已知的一类数学对象的性质类比迁移到另一类数学对象上去.一般步骤:①找出两类事物之间的相似性或者一致性.②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(或猜想).


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三上学期期中考试理科数学 题型:选择题
设Rt△ABC的三边分别为a,b,c,其中c为斜边,m]直线ax+by+c=0与圆 ,(
,(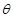 为常数,
为常数,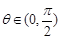 )交于
)交于 两点,则
两点,则
A.sinθ B.2sinθ C.tanθ D.2tanθ
查看答案和解析>>
科目:高中数学 来源: 题型:
设![]() 的三边分别为
的三边分别为![]() ,
,![]() ,
,![]() ,
,![]() 面积为S ,内切圆半径为
面积为S ,内切圆半径为![]() ,则
,则![]() ,类比这个结论可知:四面体
,类比这个结论可知:四面体![]() 的四个面面积分别为
的四个面面积分别为![]() ,内切球半径为
,内切球半径为![]() ,四面体
,四面体![]() 的体积为
的体积为![]() ,则
,则![]() = ( )
= ( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com