
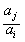 两数中至少有一个属于A,
两数中至少有一个属于A,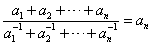 ;
;(Ⅰ)解:由于3×4与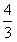 均不属于数集{1,3,4},所以该数集不具有性质P.
均不属于数集{1,3,4},所以该数集不具有性质P.
由于1×2,1×3,1×6,2×3, 都属于数集{1,2,3,6},所以该数集具有性质P.
都属于数集{1,2,3,6},所以该数集具有性质P.
(Ⅱ)证明:因为A={a1,a2,…,an}具有性质P,所以anan与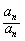 中至少有一个属于A.
中至少有一个属于A.
由于1≤a1<a2<…<an,所以anan>an,故anan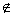 A,
A,
从而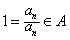 ,故a1=1;
,故a1=1;
因为1=a1<a2<…<an,所以akan>an,故akan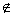 A(k=2,3,…,n).
A(k=2,3,…,n).
由A具有性质P可知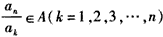 ,
,
又因为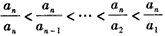 ,
,
所以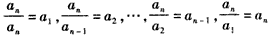 ,
,
从而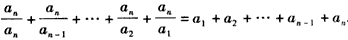 ,
,
故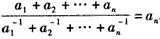 。
。
(Ⅲ)证明:由(Ⅱ)知,当n=5时,有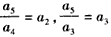 ,即
,即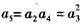 ,
,
因为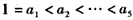 ,
,
所以![]() ,故
,故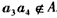 ,
,
由A具有性质P可知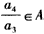 ,
,
由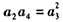 ,得
,得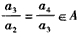 ,且
,且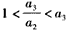 ,
,
所以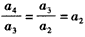 ,
,
故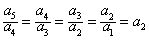 ,
,
即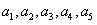 是首项为1,公比为a2的等比数列。
是首项为1,公比为a2的等比数列。


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
| aj |
| ai |
| a1+a2+…+an | ||||||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| aj | ai |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| n | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com