
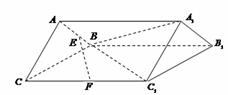
如图,三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是以
是以![]() 为底边的等腰三角形,平面
为底边的等腰三角形,平面![]() 平面
平面![]() ,
,![]() 分别为棱
分别为棱![]() 、
、![]() 的中点
的中点
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 为整数,且
为整数,且![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
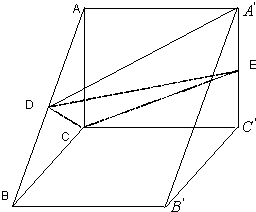 如图,三棱柱中,平面AC′⊥面BB′C′C,∠CC′B′=60°,BC=CC′AC=2,点D、E分别为棱AB,A′C′的中点
如图,三棱柱中,平面AC′⊥面BB′C′C,∠CC′B′=60°,BC=CC′AC=2,点D、E分别为棱AB,A′C′的中点查看答案和解析>>
科目:高中数学 来源: 题型:
(08年贵阳市适应性考试理) 如图,直三棱柱![]() 中,
中,![]() 为棱
为棱![]() 上的一动点,
上的一动点,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的重心.
的重心.
(1)求证:![]() ;
;
(2)若点![]() 在
在![]() 上的正射影正好为M,
上的正射影正好为M,
()求二面角![]() 的大小
的大小
() 求点![]() 到平面
到平面![]() 的距离
的距离

查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市高三上学期补考数学试卷(解析版) 题型:解答题
如图,三棱柱 中,侧面
中,侧面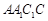
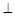 底面
底面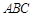 ,
,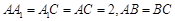 ,且
,且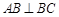 ,O为
,O为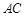 中点.
中点.
(Ⅰ)证明: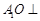 平面
平面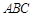 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值
所成角的正弦值

查看答案和解析>>
科目:高中数学 来源:2013届北京市高二下学期期中理科数学试卷(解析版) 题型:解答题
如图,三棱柱 中,
中, ⊥面
⊥面 ,
, ,
,
 ,
, 为
为 的中点.
的中点.
(Ⅰ)求证: ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)在侧棱 上是否存在点
上是否存在点 ,使得
,使得
 ?请证明你的结论.
?请证明你的结论.

查看答案和解析>>
科目:高中数学 来源:2011年辽宁省锦州市高一第一学期末数学卷 题型:解答题
(本小题满分12分)
如图, 在三棱柱 中,
中,  底面
底面 ,
, ,
,  ,
, , 点D是
, 点D是 的中点.
的中点.

(Ⅰ) 求证 ; (Ⅱ)
求证
; (Ⅱ)
求证 ∥平面
∥平面
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com