
思路解析:可以求出交点坐标,再利用两点间的距离公式求解;也可以利用弦长公式.
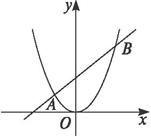
解法一:先求交点A、B,如图
解方程组y=x+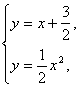 消去y,
消去y,
得x2-2x-3=0.
解得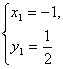 或
或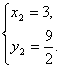 ∴A(-1,
∴A(-1,![]() )、B(3,
)、B(3,![]() ).
).
直线被曲线截得的线段长|AB|=![]() =4
=4![]() .
.
解法二:设交点的坐标A(x1,y1)、B(x2,y2),则y1=x1+![]() ,y2=x2+
,y2=x2+![]() .
.
∴y1-y2=x1-x2.由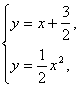 消去y,得x2-2x-3=0.
消去y,得x2-2x-3=0.
∴x1+x2=2,x1x2=-3.
弦长:|AB|=![]() =
=![]()
=![]() ·
·![]() =
=![]() ·
·![]() =4
=4![]() .
.
深化升华
解法二中设出了交点坐标,但未求交点坐标,这是应用了“设而不求”的解题技巧,要注意掌握.
一般地,设直线l的方程:y=kx+b,曲线C的方程:F(x,y)=0,
直线l与曲线C的交点为A(x1,y1)、B(x2,y2).
则y1=kx1+b,y2=kx2+b,∴y1-y2=k(x1-x2).
由![]() 消去y,得ax2+mx+c=0.∴x1+x2=-
消去y,得ax2+mx+c=0.∴x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
∴|AB|=![]() =
=![]()
=![]() =
=![]() ·
·![]() .
.
这个式子就是求弦长公式,以后在解圆锥曲线有关问题时要经常用到.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
 (2012•杨浦区二模)如图,椭圆C1:
(2012•杨浦区二模)如图,椭圆C1:| x2 |
| 4 |
| S1 |
| S2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4cosθ |
| sin2θ |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com