
如图,三棱柱ABD-A1B1D1是长方体ABCD-A1B1C1D1沿对角面BDD1B1所截而成,AA1=A1D1=![]() AB,点P在A1B1上,且A1P=
AB,点P在A1B1上,且A1P=![]() A1B1,求异面直线AP与A1D所成角的余弦值.
A1B1,求异面直线AP与A1D所成角的余弦值.

|
解:如图,以侧面BDD1B1为连接面补上一个相同的三棱柱使之还原成长方体. 连接B1C,则B1C∥A1D.在AB上取点Q,使BQ=A1P. 因为A1B1=AB,所以PB1=AQ. 又因为PB1∥AQ, 所以四边形APB1Q是平行四边形, 所以AP∥QB1. 连接CQ,设AB=4,由题可知,QB=1,BB1=BC=2, 所以QB1=QC= 在等腰三角形QB1C中,取B1C的中点O,连接QO, 则QO⊥B1C,B1O= 所以,在Rt△QOB1中, cos∠QB1C=cos∠QB1O=
点评:本题中给出的几何体是由同学们所熟知的长方体切割而成,所以通过补体还原可帮助解题.长方体中有很多平行关系,它使直线的平移更直观、方便. |


科目:高中数学 来源: 题型:
 (2013•陕西)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=
(2013•陕西)如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=AA1=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•安庆三模)如图,三棱柱ABC-A1B1C1的侧棱与底面ABC垂直,底面ABC是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G
(2013•安庆三模)如图,三棱柱ABC-A1B1C1的侧棱与底面ABC垂直,底面ABC是等腰直角三角形,∠ACB=90°,侧棱AA1=2,D、E分别是CC1与A1B的中点,点E在平面ABD上的射影是△ABD的垂心G查看答案和解析>>
科目:高中数学 来源:黑龙江省大庆实验中学2011届高三上学期期末考试数学理科试题 题型:044
如图,三棱柱ABC-A1B1C1的底面是边长为2的正三角形,且AA1⊥平面ABC,D是侧棱CC1的中点,直线AD与侧面BB1C1C所成的角为45°.

(Ⅰ)求二面角A―BD―C的余弦值;
(Ⅱ)求点C到平面ABD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图, 四棱柱ABCD-A1B1C1D1的底面ABCD是正方形, O为底面中心, A1O⊥平面ABCD, ![]() .
.
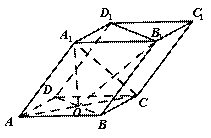
(Ⅰ) 证明: A1BD // 平面CD1B1;
(Ⅱ) 求三棱柱ABD-A1B1D1的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com