
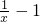
 .
. =
= ,x>0.
,x>0. -1=
-1= .
. ,即ma-
,即ma- <0对于任意的a∈(-1,1)恒成立.
<0对于任意的a∈(-1,1)恒成立. 解得-
解得- ≤m≤
≤m≤ .
. ,
, ].
]. -1≥f(1)=0,
-1≥f(1)=0, ,以x2替代x,得lnx2≥1-
,以x2替代x,得lnx2≥1- .
. +1-
+1- +…+1-
+…+1-
 +
+ +…+
+…+ ).
). +
+ +…+
+…+ <1+
<1+ +
+ +…+
+…+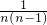
 +
+ +…+
+…+ )>-[1+
)>-[1+ +
+ +…+
+…+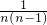 ]
] +
+ +…+
+…+ )>n-[1+
)>n-[1+ +
+ +…+
+…+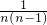 ]=n-[1+1-
]=n-[1+1- +
+ -
- +…+
+…+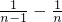 ]=
]= ,
, .
. (ln1+ln2+…+lnn)2>
(ln1+ln2+…+lnn)2> .
. .
. <0对于任意的a∈(-1,1)恒成立,即可求m的取值范围;
<0对于任意的a∈(-1,1)恒成立,即可求m的取值范围; .再利用叠加及放缩,可得ln1+ln2+…+lnn>
.再利用叠加及放缩,可得ln1+ln2+…+lnn> 恒成立,再结合柯西不等式即可证明不等式成立.
恒成立,再结合柯西不等式即可证明不等式成立.

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2(x-1) |
| x+1 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| a |
| ||
| x |
| 6 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com