
思路分析:用数学归纳法解几何问题.
证明:(Ⅰ)当n=1时,1个圆将平面分成2部分,而2=12-1+2,
∴当n=1时命题正确.
(Ⅱ)假设n=k时命题正确,即满足条件的k个圆将平面划分成k2-k+2部分,
∴当n=k+1时,平面上增加了第k+1个圆,它与原来的k个圆的每一个圆都相交于两个不同点,共2k个交点.而这2k个点将第k+1个圆分成2k段弧,每段弧将原来的一块区域隔成了两块区域,∴区域的块数增加了2k块,
∴k+1个圆将平面划分成的块数为
(k2-k+2)+2k=k2+k+2=(k+1)2-(k+1)+2,
∴n=k+1时命题也正确,
根据(Ⅰ)(Ⅱ)知命题对n∈N*都正确.
误区警示
用数学归纳法证明几何问题是教材中一种题型,但由于这种题型的证明主要是文字推理为主,所以语言一定精确,要能准确地描述第二步的假设,合理清晰地推导出结论.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源:2010年高考试题分项版理科数学之专题十七选修系列 题型:解答题
21(从以下四个题中任选两个作答,每题10分)
(1)几何证明选讲
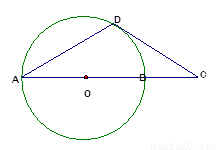
AB是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线交AB延长线于C,若DA=DC,求证AB=2BC
(2)矩阵与变换
在平面直角坐标系xOy中,A(0,0),B(-3,),C(-2,1),设k≠0,k∈R,M=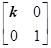 ,N=
,N=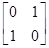 ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
(3)参数方程与极坐标
在极坐标系中,圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值
(4)不等式证明选讲
已知实数a,b≥0,求证:
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题九立体几何 题型:解答题
21(从以下四个题中任选两个作答,每题10分)
(1)几何证明选讲
AB是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线交AB延长线于C,若DA=DC,求证AB=2BC

(2)矩阵与变换
在平面直角坐标系xOy中,A(0,0),B(-3,),C(-2,1),设k≠0,k∈R,M= ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
(3)参数方程与极坐标
在极坐标系中,圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值
(4)不等式证明选讲
已知实数a,b≥0,求证:
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题三数列 题型:解答题
21(从以下四个题中任选两个作答,每题10分)
(1)几何证明选讲
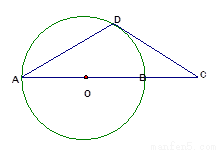
AB是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线交AB延长线于C,若DA=DC,求证AB=2BC
(2)矩阵与变换
在平面直角坐标系xOy中,A(0,0),B(-3,),C(-2,1),设k≠0,k∈R,M=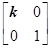 ,N=
,N=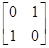 ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
(3)参数方程与极坐标
在极坐标系中,圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值
(4)不等式证明选讲
已知实数a,b≥0,求证: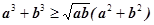
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(江苏卷)数学试题 题型:解答题
21(从以下四个题中任选两个作答,每题10分)
(1)几何证明选讲
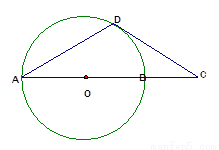
AB是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线交AB延长线于C,若DA=DC,求证AB=2BC
(2)矩阵与变换
在平面直角坐标系xOy中,A(0,0),B(-3,),C(-2,1),设k≠0,k∈R,M=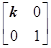 ,N=
,N=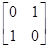 ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
(3)参数方程与极坐标
在极坐标系中,圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值
(4)不等式证明选讲
已知实数a,b≥0,求证: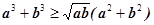
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com