
知点F(1,0),直线l:x=-1,点E是l上的动点,过点E垂直于y轴的直线与线段EF的垂直平分线交于点W.
(1)求点W(x,y)的轨迹C的方程.
(2)过点A(2,0)的直线![]() 与轨迹C交于P、Q两点,且
与轨迹C交于P、Q两点,且![]() +
+![]() =
=![]() ,求点R的轨迹方程.
,求点R的轨迹方程.
|
解析:(1)连结WF, ∵W位于线段EF的垂直平分线上, ∴|FW|=|WE|, ∴点W的轨迹是以F为焦点,以直线l为准线的抛物线. ∵p=2,∴点W(x,y)的轨迹C的方程为y2=4x. (2)设P(x1,y1),Q(x2,y2),R(x,y), ∵ ∴x1+x2-2=x-1,y1+y2=y, 又y12=4x1,y22=4x2两式相减得(y1+y2)(y1-y2)=4(x1-x2),当x1≠x2时,y· 又由平行四边形的性质得FR的中点M(也是QP的中点)在直线QR上. kQR=kAM,即 把①代入②得y· |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年丰台区统一练习一理)(13分)
已知如图(1),正三角形ABC的边长为2a,CD是AB边上的高,
E、F分别是AC和BC边上的点,且满足![]() ,现将△ABC
,现将△ABC
沿CD翻折成直二面角A-DC-B,如图(2).
(Ⅰ) 试判断翻折后直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ) 求二面角B-AC-D的大小;
(Ⅲ) 若异面直线AB与DE所成角的余弦值为![]() ,求k的值.
,求k的值.
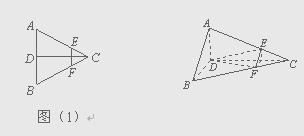
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:高考真题 题型:解答题
 =
= ,求△BDK的内切圆M的方程。
,求△BDK的内切圆M的方程。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com