
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别是AE,AB的中点.

(1)求证:PQ∥平面ACD;
(2)求AD与平面ABE所成的角的正弦值.
|
(1)证明:在△ABE中,P,Q分别是AE,AB的中点, 所以PQ∥EB,且PQ= 又EB∥DC,所以PQ∥DC. 因为PQ 所以PQ∥平面ACD. (2)解:连接DP,CQ.在△ABC中,AC=BC=2,AQ=BQ,所以CQ⊥AB. 因为DC⊥平面ABC,EB∥DC, 所以EB⊥平面ABC,所以EB⊥CQ. 因为AB∩EB=B,所以CQ⊥平面ABE. 由(1)知PQ∥DC,且PQ= 所以DP⊥平面ABE,则AD在平面ABE内的射影是AP,所以AD与平面ABE所成的角是∠DAP. 由AC=BC=2,∠ACB=120°,得∠CAQ=30°, 则DP=CQ=2sin∠CAQ=1. 又AD= 所以sin∠DAP= 即AD与平面ABE所成的角的正弦值为 点评:用定义求直线与平面所成的角时,应注意:(1)先判断直线与平面的位置关系.(2)当直线是平面的斜线时,常用以下步骤:①作出或找到斜线与其射影所成的角;②论证所作或找到的角为所求的角;③用解三角形的方法求角;④点明斜线与平面所成的角.找两条异面直线所成的角,可通过平行移动(作平行线),把两条异面直线所成的角转化为两条相交直线所成的角.二面角主要用定义法求解. |


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
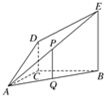 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
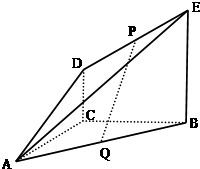 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=90°,P、Q分别为DE、AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=90°,P、Q分别为DE、AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
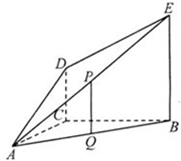 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
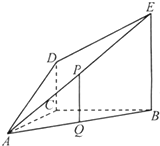 如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.
如图,DC⊥平面ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q分别为AE,AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com