

图1-4-16
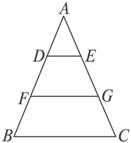
思路分析:由数形结合易知,△ABC是直角三角形,AF为斜边上的高线,CF是直角边AC在斜边上的射影,AC为所求,已知的另外两边都在△BDC中,且BD=DC=1,即△BDC是等腰三角形.因此,可以过D作DE⊥BC,拓开思路.由于DE、AF同垂直于BC,又可以利用比例线段的性质,逐步等价转化求得AC.
解:在△ABC中,设AC为x,
∵AB⊥AC,AF⊥BC,又FC=1,根据射影定理,得AC2=FC·BC,即BC=x2.?
再由射影定理,得AF2=BF·FC=(BC-FC)·FC,即![]() .
.
∴![]() =x2-1.?
=x2-1.?
在△BDC中,过D作DE⊥BC于E,?
∵BD =DC=1,∴BE=EC.?
又∵AF⊥BC,∴DE∥AF.?
∴![]() =
=![]() .?
.?
∴![]() =
=![]() .?
.?
在Rt△DEC中,∵DE2 + EC2 = DC2,?
即![]() +
+![]() =12,∴
=12,∴![]() +
+![]() =1.?
=1.?
由![]() =
=![]() ,
, ![]() =
=![]() ,整理得x6=4.
,整理得x6=4.
∴![]() .?
.?
∴![]() .
.


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 100 |
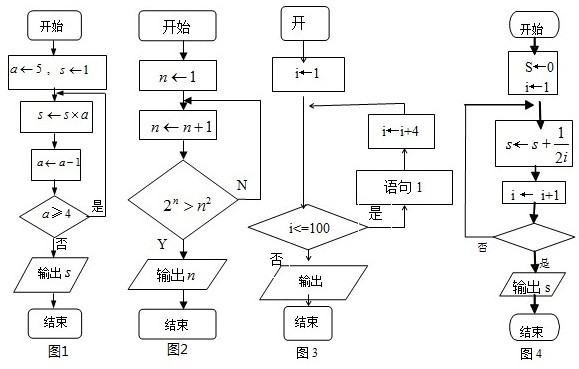
查看答案和解析>>
科目:高中数学 来源: 题型:
 用长为16米的篱笆借助一墙角围成一个矩形ABCD(如图所示),在P处有一棵树距两墙的距离分别为a(0<a<12)米和4米,现需要将此树圈进去,设矩形ABCD的面积为y(平方米),长BC为x(米).
用长为16米的篱笆借助一墙角围成一个矩形ABCD(如图所示),在P处有一棵树距两墙的距离分别为a(0<a<12)米和4米,现需要将此树圈进去,设矩形ABCD的面积为y(平方米),长BC为x(米).查看答案和解析>>
科目:高中数学 来源: 题型:
图
查看答案和解析>>
科目:高中数学 来源: 题型:
A.4 B![]() D.
D.![]()

图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com