
如下图,AB是圆O的直径,PA垂直于圆O所在平面,M是圆周上任意一点,AN⊥PM,垂足为N.

求证:AN⊥平面PBM.
|
证明:∵PA⊥平面ABM,BM ∴PA⊥BM. 又AB是圆O的直径,可得AM⊥BM, ∵PA∩AM=A,∴BM⊥平面PAM. ∴BM⊥AN. ∴AN与PM、BM两条相交直线垂直. ∴AN⊥平面PBM. 思路分析:本题考查线面垂直的定义,以及证明线面垂直的方法.要证线面垂直,需证直线和平面内的两条相交直线都垂直.已知AN⊥PM,只要再证AN和平面PBM内的另一条直线,如BM或PB垂直即可. 再结合已知中线面垂直,可找线线垂直. 温馨提示:判定一条直线和一个平面垂直有以下两种方法: (1)利用定义,即证这条直线和平面内的任意一条直线垂直.由于要垂直平面内的任意一条直线,具有不确定性,这给我们的证明带来了不便,因此这个方法的操作性不很强. (2)利用线面垂直的判定定理证明线面垂直可以转化为直线和直线垂直问题.另一方面,证明线线垂直,由于直线和平面垂直时,直线和这个平面内的所有直线都垂直,因此证明垂直问题的过程实质是线线垂直和线面垂直的相互转化的过程. |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:江苏省常州高级中学2007~2008学年第三次阶段教学质量调研高三数学(理科) 题型:044
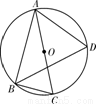
如下图所示,AB是圆O的直径,![]() ,AB=10,BD=8,求cos∠BCE的值.
,AB=10,BD=8,求cos∠BCE的值.

查看答案和解析>>
科目:高中数学 来源:广东省广州市2012届高三上学期调研测数学理科试卷 题型:022
(几何证明选讲选做题)如下图,AB是圆O的直径,直线CE与圆O相切于点C,AD⊥CE于点D,若圆O的面积为4π,∠ABC=30°,则AD的长为________.

查看答案和解析>>
科目:高中数学 来源:广东省广州市2012届高三上学期调研测数学文科试卷 题型:022
(几何证明选讲选做题)如下图,AB是圆O的直径,直线CE与圆O相切于点C,AD⊥CE于点D,若圆O的面积为4π,∠ABC=30°,则AD的长为________.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省十二校高三第一次联考数学理卷 题型:填空题
.如下图,AC是⊙O的直径,B是圆上一点,∠ABC的平分线与⊙O相交于D,已知BC=1,AB=,则AD= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com