
 ”的概率是 .
”的概率是 . 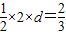 ,知P到正方形四边的距离均大于
,知P到正方形四边的距离均大于 ,从而确定出P所在的区域,用P点所在区域的面积除以正方形ABCD的面积即可.
,从而确定出P所在的区域,用P点所在区域的面积除以正方形ABCD的面积即可.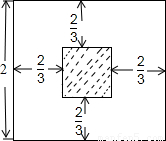 解:如图,点P在正方形ABCD内部,同时保证“△PAB、△PBC、△PCD、△PDA的面积均大于
解:如图,点P在正方形ABCD内部,同时保证“△PAB、△PBC、△PCD、△PDA的面积均大于 ”,则需要点P到正方形的四条边的距离均大于
”,则需要点P到正方形的四条边的距离均大于 ,
, 为边长的正方形区域内,且小正方形的每一条边到与它相邻的大正方形的边的距离为
为边长的正方形区域内,且小正方形的每一条边到与它相邻的大正方形的边的距离为 ,
,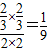 .
. .
.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
 如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.
如图,正方形ABCD的边长为1,正方形ADEF所在平面与平面ABCD互相垂直,G,H是DF,FC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| MN |
| OM |
| ON |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com