
如图,已知
AM、BN、CP、DQ分别是四面体ABCD的高,且AM、BN相交.求证:CP、DQ相交.
|
设 AM与BN确定的平面为a.∵AA⊥平面BCD,∴AM⊥CD.同理BN⊥CD,∴CD⊥平面a又AB 平面a,∵AB⊥CD.∵CP⊥平面ABD,∴CP⊥AB.∴AB⊥平面CDP(如图).又AB 平面a,∵AB⊥CD.∵CP⊥平面ABD,∴CP⊥AB.∴AB⊥平面CDP(如图).又AB 平面ABC,∴平面ABC⊥平面CDP.∵DQ⊥平面ABC,根据结论:如果两个平面互相垂直,那么经过第一个平面内一点垂直于第二个平面的直线在第一个平面内.∴DQ 平面ABC,∴平面ABC⊥平面CDP.∵DQ⊥平面ABC,根据结论:如果两个平面互相垂直,那么经过第一个平面内一点垂直于第二个平面的直线在第一个平面内.∴DQ 平面CDP.∵CP、DQ在一个平面内且不平行,∴CP与DQ必相交.判定直线在平面内,课本(包括例题、习题)中出现的结论有:①若一条直线上的两点在一个平面内,则这条直线上所有点都在这个平面内;②过一点与已知直线垂直的直线,都在过这点与已知直线垂直的平面内;③过平面外一点与已知平面平行的直线,都在过这点与已知平面平行的平面内;④一直线平行于一平面,则过平面内一点与已知直线平行的直线都在该平面内;⑤两平面垂直,过第一个平面内一点垂直于第二个平面的直线在第一个平面内.要证CP、DQ相交,只需证CP、DQ在同一个平面内,这个平面应该CD与CP所确定的平面.因此,只需证明DQ在平面CDP中,因为DQ⊥面ABC,因此只需证平面CDP⊥面ABC. 平面CDP.∵CP、DQ在一个平面内且不平行,∴CP与DQ必相交.判定直线在平面内,课本(包括例题、习题)中出现的结论有:①若一条直线上的两点在一个平面内,则这条直线上所有点都在这个平面内;②过一点与已知直线垂直的直线,都在过这点与已知直线垂直的平面内;③过平面外一点与已知平面平行的直线,都在过这点与已知平面平行的平面内;④一直线平行于一平面,则过平面内一点与已知直线平行的直线都在该平面内;⑤两平面垂直,过第一个平面内一点垂直于第二个平面的直线在第一个平面内.要证CP、DQ相交,只需证CP、DQ在同一个平面内,这个平面应该CD与CP所确定的平面.因此,只需证明DQ在平面CDP中,因为DQ⊥面ABC,因此只需证平面CDP⊥面ABC. |


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
 如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=
如图,直线l1和l2相交于点M且l1⊥l2,点N∈l1.以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=| 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
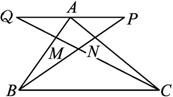
如图,已知△ABC,在AC上取点N,使AN=![]() AC,在AB上取点M,使AM=
AC,在AB上取点M,使AM=![]() AB,在BN的延长线上取点P,使NP=
AB,在BN的延长线上取点P,使NP=![]() BN,在CM的延长线上取点Q,使MQ=
BN,在CM的延长线上取点Q,使MQ=![]() CM,用向量的方法证明P、A、Q三点共线.
CM,用向量的方法证明P、A、Q三点共线.
 ??
??
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com