Question

某种细胞每隔1小时死亡3个，其余的细胞每个分裂成两个.若最初有9个细胞，n小时后细胞的个数记为a_n.

(1)求a_n关于n的表达式f(n);

(2)多少时间后细胞的个数超过1 000个？

Answer 1

解：(1)a₁=9,a_n=2(a_n-1-3),

即a_n=2a_n-1-6,                          ①

a_n+1=2a_n-6.                            ②

②-①,a_n+1-a_n=2(a_n-a_n-1).

令b_n=a_n+1-a_n,则b_n是以b₁=a₂-a₁=12为首项，2为公比的等比数列.

∴b_n=12×2^n-1=3·2ⁿ⁺¹.

∴a_n+1-a_n=3·2ⁿ⁺¹.

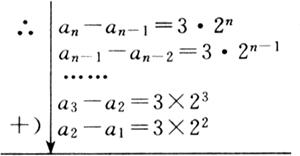
    a_n-a₁=3·(2ⁿ+2^n-1+…+2)=3·(2ⁿ-1),

∴a_n=6+3·2ⁿ.

(2)假设n小时后细胞的个数超过1 000个，

则a_n＞1 000,即6+3·2ⁿ＞1 000，

∴2ⁿ＞.

两边取以2为底的对数得，

n＞log₂，

而2⁸=256＜＜512=2⁹.

又∵n∈N^*,∴n=9.

∴9小时后细胞的个数超过1 000个.