
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:
(12分)如图①,在等腰梯形![]() 中,已知
中,已知![]() 均为梯形的高,且
均为梯形的高,且![]() 。现沿
。现沿![]() 将
将![]() 和
和![]() 折起,使点
折起,使点![]() 重合为一点
重合为一点![]() ,如图②所示。又点
,如图②所示。又点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() 。
。
 (1)求线段
(1)求线段![]() 的长;
的长;
(2)求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)如图,在等腰梯形![]() 中,已知
中,已知![]() 均为梯形的高,且
均为梯形的高,且![]() 。现沿
。现沿![]() 将
将![]() 和
和![]() 折起,使点
折起,使点![]() 重合为一点
重合为一点![]() ,如图②所示。又点
,如图②所示。又点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() 。
。
(1)求线段![]() 的长;
的长;
(2)求二面角![]() 的大小。
的大小。

查看答案和解析>>
科目:高中数学 来源:2013-2014学年山西省高三上学期期中考试理科数学试卷(解析版) 题型:解答题
如图1,在直角梯形 中,
中,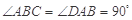 ,
,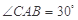 ,
,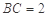 ,
,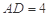 . 把
. 把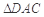 沿对角线
沿对角线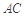 折起到
折起到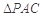 的位置,如图2所示,使得点
的位置,如图2所示,使得点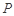 在平面
在平面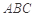 上的正投影
上的正投影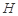 恰好落在线段
恰好落在线段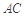 上,连接
上,连接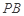 ,点
,点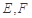 分别为线段
分别为线段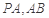 的中点.
的中点.
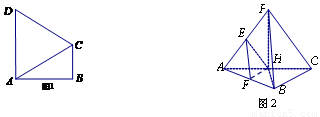
(1)求证:平面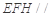 平面
平面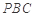 ;
;
(2)求直线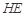 与平面
与平面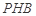 所成角的正弦值;
所成角的正弦值;
(3)在棱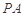 上是否存在一点
上是否存在一点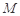 ,使得
,使得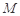 到点
到点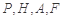 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年北京市海淀区高三5月期末练习(二模)理科数学试卷(解析版) 题型:解答题
如图1,在直角梯形 中,
中, ,
, ,
,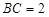 ,
,
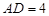 . 把
. 把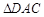 沿对角线
沿对角线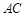 折起到
折起到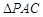 的位置,如图2所示,使得点
的位置,如图2所示,使得点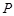 在平面
在平面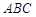 上的正投影
上的正投影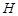 恰好落在线段
恰好落在线段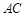 上,连接
上,连接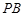 ,点
,点 分别为线段
分别为线段 的中点.
的中点.
(I)求证:平面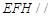 平面
平面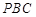 ;
;
(II)求直线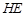 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(III)在棱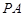 上是否存在一点
上是否存在一点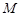 ,使得
,使得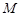 到点
到点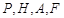 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com