
思路分析:本题所证不等式为对称式(任意互换两个字母,不等式不变),在处理该类式子中,经常对每个式子采用同样的处理方法即可(即轮换技巧).中间式子中每项均为两个式子的和,将它们拆开,再用排序不等式证明.
证明:不妨设a≥b≥c,则a2≥b2≥c2,![]() ≥
≥![]() ≥
≥![]() ,则a2·
,则a2·![]() +b2·
+b2·![]() +c2·
+c2·![]() (乱序和)≥a2·
(乱序和)≥a2·![]() +b2·
+b2·![]() +c2·
+c2·![]() (倒序和),同理a2·
(倒序和),同理a2·![]() +b2·
+b2·![]() +c2·
+c2·![]() (乱序和)≥a2·
(乱序和)≥a2·![]() +b2·
+b2·![]() +c2·
+c2·![]() (倒序和).两式相加再除以2,即得原式中第一个不等式.再考虑数组a3≥b3≥c3及
(倒序和).两式相加再除以2,即得原式中第一个不等式.再考虑数组a3≥b3≥c3及![]() ≥
≥![]() ≥
≥![]() ,仿上可证第二个不等式.
,仿上可证第二个不等式.
方法归纳
证明不等式就是对不等式的左右两边或条件与结论进行代数变形和化归,这些操作包括一些添项、拆项,及一定的构造,而变形的主要依据是不等式的性质.因此在学习中,应该认真把握这个定理的内容形式.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| 1-x |
| x |
| 1-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
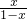 ≥|
≥|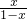 |},C={x|ax2+x+b<0},
|},C={x|ax2+x+b<0},查看答案和解析>>
科目:高中数学 来源:湖南省月考题 题型:解答题
 ≥|
≥| |},C={x|ax2+x+b<0},
|},C={x|ax2+x+b<0}, ,A∪B∪C=R,求实数a、b的值.
,A∪B∪C=R,求实数a、b的值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖南省邵阳市洞口二中高三(下)3月月考数学试卷(文科)(解析版) 题型:解答题
 ≥|
≥| |},C={x|ax2+x+b<0},
|},C={x|ax2+x+b<0},查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com