
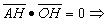 .
. 解:由![]() ,连AH并延长交BC于M.
,连AH并延长交BC于M.
则由H为△ABC的垂心.∴AM⊥BC.
于是BC⊥平面OAH![]() OH⊥BC.
OH⊥BC.
同理可证:![]()
又![]() 是空间中三个不共面的向量,由向量基本定理知,存在三个实数k1,k2,k3使得
是空间中三个不共面的向量,由向量基本定理知,存在三个实数k1,k2,k3使得![]() =k1a+k2b+k3c.
=k1a+k2b+k3c.
由![]() =0且a·b=a·c=0
=0且a·b=a·c=0![]() k2b2=k3c2,同理k1a2=k2b2.
k2b2=k3c2,同理k1a2=k2b2.
∴k1a2=k2b2=k3c2=m≠0.①又AH⊥OH,
∴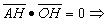
(k1-1)a+k2b+k3c(k1a+k2b+k3c)=0![]() k1(k1-1)a2+k22b2+k32c2=0②?
k1(k1-1)a2+k22b2+k32c2=0②?
联立①及②,得
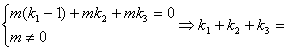 1③
1③
又由①,得k1=![]() ,k2=
,k2=![]() ,k3=
,k3=![]() ,代入③得
,代入③得
m=![]()
![]()
![]() ,?
,?
其中Δ=a2·b2+b2·c2+c2·a2,于是![]() =
=![]() (b2·c2·a+c2·a2·b+a2·b2·c).
(b2·c2·a+c2·a2·b+a2·b2·c).


科目:高中数学 来源: 题型:
| OA |
| BC |
| OB |
| CA |
| OC |
| AB |
| A、外心 | B、内心 | C、垂心 | D、重心 |
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学必修4 2.5向量的应用练习卷(解析版) 题型:选择题
已知O为△ABC所在平面内一点,满足
 ,则点O是△ABC的(
)
,则点O是△ABC的(
)
A.外心 B.内心 C.垂心 D.重心
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com