
 的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60°,
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60°,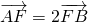 .则椭圆C的离心率为________.
.则椭圆C的离心率为________.
 解:如图,设设椭圆的左准线为l,过A点作AC⊥l于C,
解:如图,设设椭圆的左准线为l,过A点作AC⊥l于C, ,
,
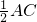 …②
…②

 .
. .
.

科目:高中数学 来源: 题型:
(09年如东热身卷)(15分)设椭圆C:![]() 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且![]() .
.
⑴求椭圆C的离心率;
⑵若过A、Q、F三点的圆恰好与直线l:![]() 相切,求椭圆C的方程.
相切,求椭圆C的方程.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省沈阳市高三高考领航考试(三)文科数学试卷(解析版) 题型:解答题
设椭圆C: 的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o, .
.
求椭圆C的离心率;
如果|AB|= ,求椭圆C的方程.
,求椭圆C的方程.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江省哈尔滨市高三上学期期末考试理科数学 题型:解答题
.设椭圆C: 的左焦点为
的左焦点为 ,上顶点为
,上顶点为 ,过点
,过点 作垂直于
作垂直于 直线交椭圆
直线交椭圆 于另外一点
于另外一点 ,交
,交 轴正半轴于点
轴正半轴于点 ,
,
且
⑴求椭圆 的离心率; (6分)
的离心率; (6分)
⑵若过 三点的圆恰好与直线
三点的圆恰好与直线
 相切,求椭圆C的方程. (6分)
相切,求椭圆C的方程. (6分)

查看答案和解析>>
科目:高中数学 来源:2013届河北省高二下学期一调考试理科数学 题型:填空题
设椭圆C: 的左焦点为F,上顶点为A,过点A作垂直于AF
的左焦点为F,上顶点为A,过点A作垂直于AF
的直线交椭圆C于另外一点P,交x轴正半轴于点Q, 且  ,则椭圆C的离心率为
,则椭圆C的离心率为
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(辽宁卷)理科数学 题型:解答题
设椭圆C: 的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o, .
.
(I) 求椭圆C的离心率;
(II)
如果|AB|= ,求椭圆C的方程.
,求椭圆C的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com