练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在正四棱锥S－ABCD中，P在SC上，Q在SB上，R在SD上，且SP∶PC＝1∶2，SQ∶SB＝2∶3，SR∶RD＝2∶1．求证：SA∥平面PQR．

    答案：
    解析：

    　　证：连AC、BD，设交于O，连SO，连RQ交SO于M，取SC中点N，连ON，那么ON∥SA．

    　　∵＝＝

    　　∴RQ∥BD

    　　∴＝而＝

    　　∴＝　∴PM∥ON

    　　∵SA∥ON．∴SA∥PM，PM平面PQR

    　　∴SA∥平面PQR．

    　　评析：利用平几中的平行线截比例线段定理．

    　　三角形的中位线性质等知识促成“线线平行”向“线面平行”的转化．


    提示：

    根据直线和平面平行的判定定理，必须在平面PQR内找一条直线与AS平行即可．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

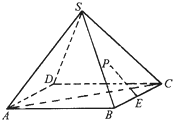    如图，在正四棱锥S-ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE⊥AC．则动点P的轨迹与△SCD组成的相关图形是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在正四棱锥S-ABCD中，E，M，N分别是BC，CD，SC的中点，动点P在线段MN上运动时，下列四个结论中恒成立的个数为（　　）
    （1）EP⊥AC； 
    （2）EP∥BD；
    （3）EP∥面SBD；
    （4）EP⊥面SAC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，在正四棱锥S-ABCD中，AB=8
    		2
    ，SA=10，M、N、O分别是SA、SB、BD的中点．
    （1）设P是OC的中点，证明：PN∥平面BMD；
    （2）求直线SO与平面BMD所成角的大小；
    （3）在△ABC内是否存在一点G，使NG⊥平面BMD，若存在，求线段NG的长度；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年江苏省淮安市涟水县郑梁梅高中高一（上）第二次月考数学试卷（解析版） 题型：选择题

    如图，在正四棱锥S-ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE⊥AC．则动点P的轨迹与△SCD组成的相关图形是（ ）
    A．
    B．
    C．
    D．

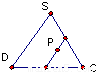
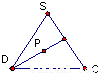
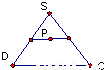
    查看答案和解析>>

    科目：高中数学 来源：2013年辽宁省沈阳市东北育才学校高考数学二模试卷（文科）（解析版） 题型：选择题

    如图，在正四棱锥S-ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE⊥AC．则动点P的轨迹与△SCD组成的相关图形是（ ）
    A．
    B．
    C．
    D．

    查看答案和解析>>

    同步练习册答案