Question

设△ABC的顶点A(1，3)，边AB、AC上的中线所在直线的方程分别为x-2y＋1=0，y=1，求△ABC中AB、AC各边所在直线的方程.

Answer 1

活动:为了搞清△ABC中各有关元素的位置状况，我们首先根据已知条件，画出图5，帮助思考问题.

解:如图8,设AC的中点为F，则AC边上的中线BF为y=1.

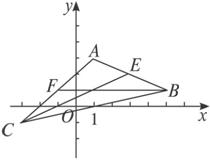
图8

AB边的中点为E，则AB边上中线CE为x-2y＋1=0.

设C点坐标为(m，n).在A、C、F三点中A点已知，C点未知，F虽为未知但其在中线BF上，满足y=1这一条件.

这样用中点公式解出n=-1.

又C点在中线CE上，应当满足CE的方程，则m-2n＋1=0.

∴m=-3.∴C点为(-3，-1).

用同样的思路去求B点.设B点为(a，b)，显然b=1.

又B点、A点、E点中，E为中点，B点为(a，1),

E点坐标为(,),即(,2).E点在CE上,应当满足CE的方程-4+1=0,解出a=5.

∴B点为(5，1).

由两点式，即可得到AB，AC所在直线的方程.l_AC:x-y＋2=0.l_AB:x＋2y-7=0.

点评：此题思路较为复杂，应使同学们做完后从中领悟到两点：

(1)中点公式要灵活应用；

(2)如果一个点在直线上，则这点的坐标满足这条直线的方程，这一观念必须牢牢地树立起来.