
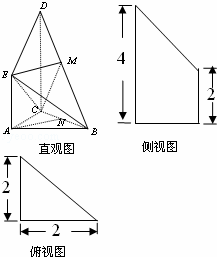
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求出该几何体的体积.
(Ⅱ)若N是BC的中点,求证:AN∥平面CME;
(Ⅲ)求证:平面BDE⊥平面BCD.
考点:
平面与平面垂直的判定;由三视图求面积、体积;直线与平面平行的判定.
分析:
(I)由图可以看出,几何体可以看作是以点B为顶点的四棱锥,其与底面积易求;
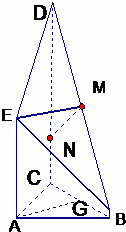
(II)证明线AN与面CME中一线平行即可利用线面平行的判定定理得出线面平行,由图形易得,可构造平行四边形证明线线平行,连接MN,则MN∥CD,AE∥CD,即可证得;
(Ⅲ)要平面BDE⊥平面BCD,关键是在一平面中寻找另一平面的垂线,易得AN⊥平面BCD,利用AN∥EM,可得EM⊥平面BCD
,从而得证
解答:
解:(Ⅰ)由题意,EA⊥平面ABC,DC⊥平面ABC,AE∥DC,AE=2,DC=4,AB⊥AC,且AB=AC=2
∵EA⊥平面ABC,
∴EA⊥AB,又AB⊥AC,∴AB⊥平面ACDE
∴四棱锥B﹣ACDE的高h=AB=2,梯形ACDE的面积S=6
∴![]() ,
,
即所求几何体的体积为4(4分)(Ⅱ)连接MN,则MN∥CD,AE∥CD
又![]() ,所以四边形ANME为平行四边形,∴AN∥EM …(6分)
,所以四边形ANME为平行四边形,∴AN∥EM …(6分)
∵AN⊄平面CME,EM⊂平面CME,所以,AN∥平面CME; …(8分)
(Ⅲ)∵AC=AB,N是BC的中点,AN⊥BC,平面ABC⊥平面BCD
∴AN⊥平面BCD …(10分)
由(Ⅱ)知:AN∥EM
∴EM⊥平面BCD
又EM⊂平面BDE
所以,平面BDE⊥平面BCD.…(12分)
点评:
本题以三视图为载体,考查几何体的体积,考查线面平行与垂直,解题的关键是由三视图得出直观图,正确利用线面平行于垂直的判定.


科目:高中数学 来源: 题型:
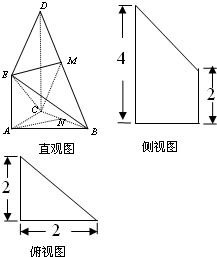 (2012•烟台三模)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(2012•烟台三模)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,M是BD的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
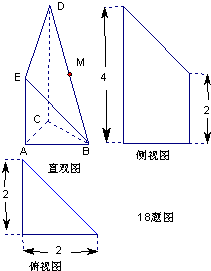 如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,M是BD的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,M是BD的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,![]() 是
是![]() 的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
![]() (Ⅰ)求出该几何体的体积;
(Ⅰ)求出该几何体的体积;
![]() (Ⅱ)求证:EM∥平面ABC;
(Ⅱ)求证:EM∥平面ABC;
![]() (Ⅲ) 试问在棱DC上是否存在点N,
(Ⅲ) 试问在棱DC上是否存在点N,
![]() 使NM⊥平面
使NM⊥平面![]() ? 若存在,确定点N的位置;
? 若存在,确定点N的位置;
![]() 若不存在,请说明理由.
若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图.在直观图中,
![]() 是
是![]() 的中点.侧视图是直角梯形,俯视图是等腰直角
的中点.侧视图是直角梯形,俯视图是等腰直角
三角形,有关数据如图所示.
(Ⅰ)求出该几何体的体积;
(Ⅱ)求证:EM∥平面ABC;
(Ⅲ) 试问在棱DC上是否存在点N,使NM⊥平面![]() ? 若存在,确定点N的位置;
? 若存在,确定点N的位置;
若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三下学期二调考试文科数学试卷(解析版) 题型:解答题
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图、俯视图,在直观图中,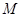 是
是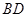 的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求出该几何体的体积。
(Ⅱ)若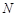 是
是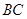 的中点,求证:
的中点,求证: 平面
平面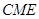 ;
;
(Ⅲ)求证:平面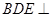 平面
平面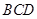 .
.
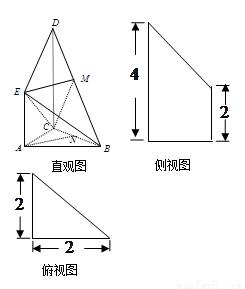
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com