
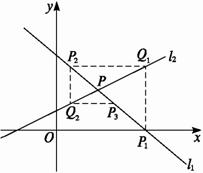
直线l1与x轴交于点P1,过点P1作x轴的垂线交直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2……这样一直作下去,可得到一系列点P1,Q1,P2,Q2,….点Pn(n=1,2,…)的横坐标构成数列{xn}.
比较2|PPn|2与4k2|PP1|2+5的大小.
解析:由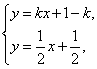 得P的坐标为(1,1).
得P的坐标为(1,1).
所以2|PPn|2=2(xn-1)2+2(kxn+1-k-1)2=8×(![]() )2n+2(
)2n+2(![]() )2n-2,?
)2n-2,?
4k2|PP1|2+5=4k2[(1-![]() -1)2+(0-1)2]+5=4k2+9.?
-1)2+(0-1)2]+5=4k2+9.?
(1)当|k|>![]() ,即k<-
,即k<-![]() 或k>
或k>![]() 时,
时,
4k2|PP1|2+5>1+9=10,?
而此时0<|![]() |<1,所以2|PPn|2<8×1+2=10.?
|<1,所以2|PPn|2<8×1+2=10.?
故2|PPn|2<4k2|PP1|2+5.?
(2)当0<|k|<![]() ,即k∈(-
,即k∈(-![]() ,0)∪(0,
,0)∪(0,![]() )时,?
)时,?
4k2|PP1|2+5<1+9=10=10,?
而此时|![]() |>1,所以2|PPn|2>8×1+2=10.?
|>1,所以2|PPn|2>8×1+2=10.?
故2|PPn|2>4k2|PP1|2+5.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
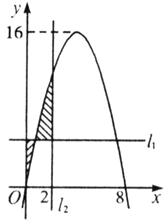
(1)求a、b、c的值;
(2)求阴影面积S关于t的函数S(t)的解析式;
(3)若g(x)=6lnx+m,问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
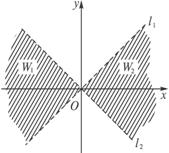
(1)分别用不等式组表示W1和W2;
(2)若区域W中的动点P(x,y)到l1、l2的距离之积等于d2,求点P的轨迹C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
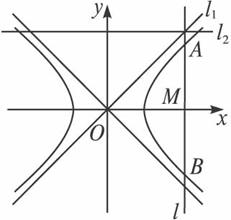
(1)求双曲线C的离心率;
(2)求双曲线C的方程.
(文)已知公差不为零的等差数列{an}的前n项和为Sn,Sn及通项an满足关系式:4Sn=an2+αan+β(α、β为常数,n∈N+),且a1=-1.
(1)求常数α、β的值;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
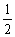
(Ⅰ)证明:xn+1-1=![]() (xn-1),n∈N*;
(xn-1),n∈N*;
(Ⅱ)求数列{xn}的通项公式;
(Ⅲ)比较2|PPn|2与4k2|PP1|2+5的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com