
 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为 ,且各次投篮互不影响。
,且各次投篮互不影响。 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两人轮流投篮直至某人投中为止,已知甲投篮每次投中的概率为0.4,乙每次投篮投中的概率为0.6,各次投篮互不影响.设甲投篮的次数为![]() ,若乙先投,且两人投篮次数之和不超过4次,求
,若乙先投,且两人投篮次数之和不超过4次,求![]() 的概率分布.
的概率分布.
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试理科数学(重庆卷解析版) 题型:解答题
甲、乙两人轮流投篮,每人每次投一票.约定甲先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为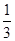 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为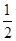 ,且各次投篮互不影响.[来(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数
,且各次投篮互不影响.[来(Ⅰ) 求甲获胜的概率;(Ⅱ)求投篮结束时甲的投篮次数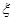 的分布列与期望
的分布列与期望
查看答案和解析>>
科目:高中数学 来源:2012年全国普通高等学校招生统一考试文科数学(重庆卷解析版) 题型:解答题
甲、乙两人轮流投篮,每人每次投一球,约定甲先投且先投中者获胜,一直每人都已投球3次时投篮结束,设甲每次投篮投中的概率为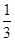 ,乙每次投篮投中的概率为
,乙每次投篮投中的概率为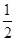 ,且各次投篮互不影响。(Ⅰ)求乙获胜的概率;(Ⅱ)求投篮结束时乙只投了2个球的概率。
,且各次投篮互不影响。(Ⅰ)求乙获胜的概率;(Ⅱ)求投篮结束时乙只投了2个球的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com