练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如下图，在△ABC中，点M是BC的中点，点N在边AC上，且AN＝2NC，AM与BN相交于点P，求AP∶PM的值．

    答案：
    解析：

    　　解：设＝e2，则

    　　

    　　∵A、P、M和B、P、N分别共线，

    　　∴存在实数λ、μ使＝－λe1－3λe2，＝2μe1＋μe2．

    　　∴＝(λ＋2μ)e1＋(3λ＋μ)e2，而＝2e1＋3e2，

    　　由基本定理，得解得

    　　∴＝，即AP∶PM＝4∶1．

    　　点评：以向量为工具来解平面几何问题是一种重要的方法．在求共线线段时，可适当选择一组基底，用这组基底可表示平面内的有关向量，再由向量共线条件列出等式，用待定系数法解之．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如下图，在△ABC中，点M是BC的中点，点N在边AC上，且AN=2NC，AM与BN相交于点P，求AP∶PM的值.

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省淄博一中高一上学期期末考试数学试卷（带解析） 题型：单选题

    如下图，在△ABC中，设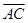＝，＝，AP的中点为Q，BQ的中点为R，CR的中点为P，若＝m＋n，则        （       ）                        

    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：2015届山东省高一上学期期末考试数学试卷（解析版） 题型：选择题

    如下图，在△ABC中，设＝，＝，AP的中点为Q，BQ的中点为R，CR的中点为P，若＝m＋n，则        （       ）                        

    A．              B．               C．               D．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如下图，在△ABC中，D、E、F分别是BC、AB、CA的中点，=a,求-+.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）如下图，在△ABC中，D为BC边上的中点.求证：=（+）.

    （2）G为△ABC重心，O为平面内不同于G的任意一点，则=（++）.

    查看答案和解析>>

    同步练习册答案