

(1)证明MF是异面直线AB与PC的公垂线;
(2)若PA=3AB,求直线AC与平面AEM所成角的正弦值.
(1)证明:∵EF∥CD,CD∥AM,
∴EF∥AM.
又AM=EF,
∴四边形AEFM为平行四边形.
∵PA⊥平面ABCD,
∴PA⊥AM.而AM⊥AD,
∴AM⊥平面PAD.从而AM⊥AE.
∴四边形AEFM为矩形.
∴MF⊥AB于M.
又AE⊥PD,AE⊥EF,
∴AE⊥平面PDC.从而MF⊥平面PDC.
∴MF⊥PC于F,因此命题成立.
(2)解:如下图,连结BD交AC于O,连结BE,过O作BE的垂线OH,垂足为H.
依题意,PD⊥平面AEM,
∴ED⊥BE.

又OH⊥BE,
∴OH∥DE.
因此OH⊥平面AEM.连结AH,则∠HAO是直线AC与平面AEM所成的角.
设AB=a,则PA=![]() AC=
AC=![]() ,
,
由Rt△ADE∽Rt△PDA,得ED=![]() ,OH=
,OH=![]() ED=
ED=![]() ,
,
∴sin∠HAO=![]() ,
,
即AC与平面AEM所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
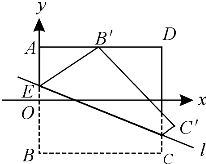 如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕,正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B′;折痕l与AB交于点E,点M满足关系式
如图,ABCD是边长为2的正方形纸片,沿某动直线l为折痕,正方形在其下方的部分向上翻折,使得每次翻折后点B都落在边AD上,记为B′;折痕l与AB交于点E,点M满足关系式| EM |
| EB |
| EB′ |
| BA |
| BF |
| PF |
| FQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
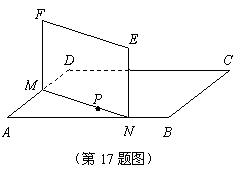
(本小题满分15分) 如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为![]() m,
m,![]() m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕
m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕![]() ,
,![]() .线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
(1) 用x的代数式表示AM;
 (2)求S关于x的函数关系式及该函数的定义域;
(2)求S关于x的函数关系式及该函数的定义域;
(3)当x取何值时,液晶广告屏幕MNEF的面积S最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
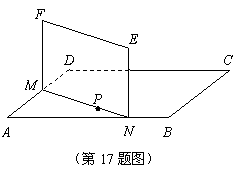
(本小题满分15分) 如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为![]() m,
m,![]() m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕
m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕![]() ,
,![]() .线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
(1) 用x的代数式表示AM;
 (2)求S关于x的函数关系式及该函数的定义域;
(2)求S关于x的函数关系式及该函数的定义域;
(3)当x取何值时,液晶广告屏幕MNEF的面积S最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD,AB距离分别为![]() m,
m,![]() m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕
m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕![]() ,
,![]() .线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).
.线段MN必须过点P,端点M,N分别在边AD,AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2). (1) 用x的代数式表示AM;(2)求S关于x的函数关系式及该函数的定义域;
(1) 用x的代数式表示AM;(2)求S关于x的函数关系式及该函数的定义域;
(3)当x取何值时,液晶广告屏幕MNEF的面积S最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com