Question

已知双曲线=1(a＞0，b＞0)的左顶点为A(-1，0)，过点A作两条直线分别交双曲线的右支于B(x₁，y₁)、C(x₂，y₂)两点，且△ABC为正三角形．

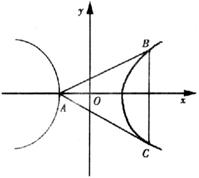
(Ⅰ)证明：B、C两点关于x轴对称；

(Ⅱ)设x₁＞2，求b的取值范围．

Answer 1

(1)证：∵|AB|=|AC|

∴(x₁+1)²+=(x₂+1)²+．

∵a=1   ∴=1

∴(x₁+1)²+b²(-1)=(x₂+1)²+b²(-1)

整理，得(x₁-x₂)[(x_l+x₂)(1+b²)+2]=0

∵x₁＞0，x₂＞0    ∴(x_l+x₂)(1+b²)+2＞0

∴x₁=x₂(5分)

∴BC⊥x轴，根据双曲线的对称性，B、C关于x轴对称

(Ⅱ)解：(法一)根据(Ⅰ)及∠A=60°，设AB的方程为y=(x+1)

代入x²-=1并整理，得(3b²-1)x²-2x-(3b²+1)=0

∵-1，x₁是方程的两根，且x₁＞2

∴3b²-1＞0，且-1·x₁=

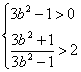∴   解得＜b²＜l

∵b＞0，∴b的取值范围为(，1)

(法二)根据(1)及∠A=60°，得y₁=(x₁+1)

∵B(x_l，y₁)在双曲线x²-=1上，

∴=1

整理得b²=

∵x₁＞2,∴0＜1+＜3, ∴＜b²＜1

∵b＞0,∴＜b＜1, ∴b的范围是（，1）.