
| 2 |
| 3 |
| OH |
| OA |
| OB |
| OC |
| OH |
| OA |
| OB |
| OC |
| OH |
| OA |
| OE |
| OH |
| OB |
| BH |
| OA |
| OC |
 过点O作垂线OD交BC与点D,并延长使得OE=2OD
过点O作垂线OD交BC与点D,并延长使得OE=2OD| OH |
| OA |
| OB |
| OC |
| OH |
| OA |
| OE |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| OH |
| OA |
| OB |
| OC |
| OH |
| OB |
| BH |
| OA |
| OC |
| BH |
| OA |
| OC |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| AM |
| AB |
| AN |
| AC |
| AO |
| AB |
| AC |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:天津市十二区县重点学校2012届高三毕业班联考(二)数学理科试题 题型:022
已知△ABC中的重心为O,直线MN过重心O,交线段AB于M,交线段AC于N其中![]() =m
=m![]() ,
,![]() =n
=n![]() ,且
,且![]() =λ
=λ![]() +μ
+μ![]() ,其中λ,μ为实数.则6 m+3n的最小值为________.
,其中λ,μ为实数.则6 m+3n的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省新余四中高三(下)开学数学试卷(理科)(解析版) 题型:选择题
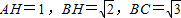 ,
,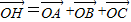 ,则S△AOB:S△BOC:S△AOC=( )
,则S△AOB:S△BOC:S△AOC=( )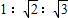
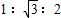
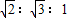

查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
已知△ABC中,O为外心,H为垂心,AH=1,BH=
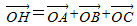 ,则S△AOB:S△BOC:S△AOC=( ) ,则S△AOB:S△BOC:S△AOC=( )
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com