Question

19.已知圆内接四边形ABCD的边长分别为AB＝2，BC＝6，CD＝DA＝4，求四边形ABCD的面积.

Answer 1

19.本小题考查三角函数的基础知识以及运用三角形面积公式及余弦定理解三角形的方法，考查运用知识分析问题、解决问题的能力.

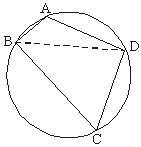
　解：如图，连结BD，则有四边形ABCD的面积

　S=S_△ABD＋S_△CBD＝AB×ADsinA+BC×CDsinC.

　∵A+C=180°，∴sinA=sinC.

∴S=(AB·AD+BC·CD)sinA

   =(2×4+6×4)sinA=16sinA.            

由余弦定理，在△ABD中，

BD²＝AB²＋AD²－2AB×ADcosA=2²+4²－2×2×4cosA=20－16cosA，

在△CDB中，

BD²＝CB²+CD²－2CB×CDcosC=6²+4²－2×6×4cosC

=52－48cosC，                            

　∴20－16cosA＝52－48cosC，

∵cosC＝－cosA，

∴64cosA=－32，

cosA=－，

∴A＝120°，

∴S＝16sin120°＝8.