Question

5．如图1所示，直角梯形ABCD，AD∥BC，AD⊥AB，AB=BC=2AD=4，E、F为线段AB、CD上的点，且EF∥BC，设AE=x，沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF（如图2所示）．
（Ⅰ）若以B、C、D、F为顶点的三棱锥体积记为f（x），求f（x）的最大值及取最大值时E的位置；
（Ⅱ）在（1）的条件下，试在线段EF上的确定一点G使得CG⊥BD，并求直线GD与平面BCD所成的角θ的正弦值．

Answer 1

分析 （Ⅰ）根据题意，证明AE⊥面BCF，求得棱锥的高，再根据体积公式求三棱锥的体积，利用配方法即可得出结论．
（Ⅱ）可利用空间向量求解，求出平面BCD的法向量，利用向量的夹角公式求直线GD与平面BCD所成的角θ的正弦值．

解答 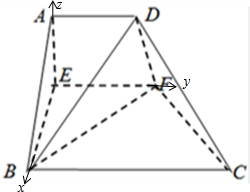解：（Ⅰ）由题意知，平面AEFD⊥平面EBCF，AE⊥EF，
所以AE⊥面BCF，…（2分）
以B、C、D、F为顶点的三棱锥底面为△BCF，高为AE，
所以$f（x）=\frac{1}{3}x\frac{1}{2}（4-x）•4=\frac{2}{3}x（4-x）=-\frac{2}{3}{（x-2）^2}+\frac{8}{3}$，…（4分）
当x=2时，$f{（x）_{max}}=\frac{8}{3}$，此时对应的点E为AB的中点．…（6分）
（Ⅱ）由（Ⅰ）中知EA、EF、EB两两互相垂直，以E为原点，以EB为x轴、EF为y轴、EA为z轴建立空间直角坐标系，则
E（0，0，0），B（2，0，0），C（2，4，0），D（0，2，2），设G（0，y_o，0）
由CG⊥BD得$\overrightarrow{GC}•\overrightarrow{BD}=（2，4-{y_o}，0）•（-2，2，2）=0$，解得y_o=2．…（8分）
所以$\overrightarrow{GD}=（0，0，2）$，设平面BCD的法向量为$\overrightarrow n=（x，y，z）$，
由$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{BD}=0\\ \overrightarrow n•\overrightarrow{BC}=0\end{array}\right.⇒\left\{\begin{array}{l}-x+y+z=0\\ y=0\end{array}\right.$，
可取$\overrightarrow{n}$=（1，0，1），
所以sinθ=|cos＜$\overrightarrow{n}$，$\overrightarrow{GD}$＞=$\frac{\sqrt{2}}{2}$即为所求．…（12分）

点评 本题考查三棱锥体积和线面角的求解．解题的关键是在求三棱锥体积时主要是高的求解这要充分分析题中条件找到高或‘等价的高'．