
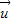 =(x,y)与向量
=(x,y)与向量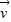 =(y,2y-x)的对应关系用
=(y,2y-x)的对应关系用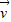 =f(
=f(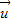 )表示.
)表示.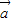 、
、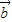 及常数m、n,恒有f(m
及常数m、n,恒有f(m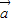 +n
+n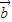 )=mf(
)=mf(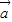 )+nf(
)+nf(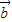 )成立;
)成立;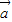 =(1,1),
=(1,1),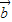 =(1,0),求向量f(
=(1,0),求向量f(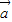 )与f(
)与f(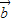 )的坐标;
)的坐标;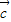 )=(p,q)(p、q为常数)的向量
)=(p,q)(p、q为常数)的向量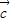 的坐标.
的坐标.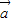 =(x1,y1),
=(x1,y1),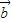 =(x2,y2),
=(x2,y2),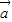 +n
+n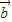 =(mx1+nx2,my1+ny2),
=(mx1+nx2,my1+ny2),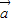 +n
+n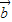 )=(my1+ny2,2(my1+ny2)-(mx1+nx2)).
)=(my1+ny2,2(my1+ny2)-(mx1+nx2)).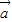 )=m(y1,2y1-x1),nf(
)=m(y1,2y1-x1),nf(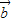 )=n(y2,2y2-x2),
)=n(y2,2y2-x2),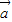 )+nf(
)+nf(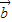 )=(my1+ny2,(2y1-x1)m+(2y2-x2)n)
)=(my1+ny2,(2y1-x1)m+(2y2-x2)n)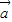 +n
+n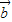 )=mf(
)=mf(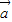 )+nf(
)+nf(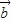 )成立.
)成立.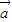 =(1,1),∴f(
=(1,1),∴f(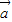 )=(1,2×1-1)=(1,1);
)=(1,2×1-1)=(1,1);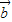 =(1,0),∴f(
=(1,0),∴f(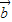 )=(0,2×0-1)=(0,-1).
)=(0,2×0-1)=(0,-1).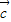 =(x,y),∴f(
=(x,y),∴f(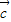 )=(y,2y-x).
)=(y,2y-x).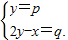
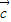 =(2p-q,p).
=(2p-q,p).

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com