练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (13分)如图(2):PA⊥面ABCD,CD2AB,

      ∠DAB=90°,E为PC的中点.

      (1)证明:BE//面PAD;

      (2)若PA=AD,证明:BE⊥面PDC.

    (1)略    (2)略


    解析:

    (1)取PD的中点M,连ME,MA.

    ∵E为PC的中点    ∴MEDC，又ABDC     ∴MEAB.即四边形ABEM为□，∴AM//BE且AM面PAD    ∴BE//面PAD.

       (2) ∵PA=AD       ∴AM⊥PD    ①

    由PA⊥面AC知:PA⊥DC，再由∠DAB=Rt∠，∴DC⊥面PAD    ∴DC⊥AM    ②

    综合①与②知: AM⊥面PDC，由(1)AM//BE   故BE⊥面PDC.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2009福建卷理）（本小题满分13分）

    如图，某市拟在长为8km的道路OP的一侧修建一条运动

    赛道，赛道的前一部分为曲线段OSM，该曲线段为函数

    y=Asinx(A>0, >0) x[0,4]的图象，且图象的最高点为

    S(3，2)；赛道的后一部分为折线段MNP，为保证参赛

    运动员的安全，限定MNP=120

    （I）求A , 的值和M，P两点间的距离；

    （II）应如何设计，才能使折线段赛道MNP最长？                                                  

    查看答案和解析>>

    科目：高中数学 来源：2013届湖北省武汉市高二下期末文科数学试卷（解析版） 题型：解答题

    （本题满分13分）

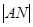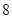    如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求B在AM上，D在AN上，对角线MN过C点，已知|AB|＝3米，|AD|＝2米，且受地理条件限制，长不超过米。

    （1）要使矩形AMPN的面积大于32平方米，则AN的长应在什么范围内？

    （2）若|AN| 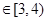（单位：米），则当AM、AN的长度是多少时，矩形花坛AMPN的面积最大？并求出最大面积．

     

    查看答案和解析>>

    科目：高中数学 来源：2014届北京师大附中高一第二学期期中考试数学试卷（解析版） 题型：解答题

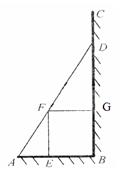
    （本题13分）如图，某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”，其中AB长为定值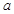,BD可长根据需要进行调节（BC足够长）。现规划在△ABD的内接正方形BEFG内种花，其余地方种草，且把种草的面积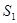与种花的面积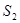的比值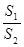称为“草花比y”。

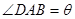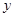    （1）设，将表示成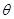的函数关系式；

    （2）当BE为多长时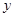，有最小值？最小值是多少？

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年福建省漳州市四地七校高三第四次联考理科数学试卷（解析版） 题型：解答题

    （本题满分13分）如图，在三棱柱中，已知

    侧面

    (Ⅰ)求直线C1B与底面ABC所成角正切值；

    (Ⅱ)在棱（不包含端点上确定一点的位置，使得(要求说明理由).

    (Ⅲ)在（2）的条件下,若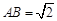，求二面角的大小.

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年福建省福州市高三第五次质量检查数学理卷 题型：解答题

    （本小题满分13分）

    如图，ABCD是块矩形硬纸板，其中AB=2AD= 2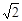，E为DC中点，将它沿AE折成直二面角D-AE-B.

    （Ⅰ）求证：AD⊥平面BDE；

    （Ⅱ）求二面角B-AD-E的余弦值.

     

     

     

    查看答案和解析>>

    同步练习册答案