
 ,8],
,8], 解:(Ⅰ)∵f(t)=log2t在t∈[ ,8]上是单调递增的,
,8]上是单调递增的,
∴log2 ≤log2t≤log28,
≤log2t≤log28,
即 ≤f(t)≤3,
≤f(t)≤3,
∴f(t)的值域G为[ ,3]。
,3]。
(Ⅱ)由题知-x2+2mx-m2+2m≤1在x∈[ ,3]上恒成立
,3]上恒成立 -2mx+m2-2m+1≥0在x∈[
-2mx+m2-2m+1≥0在x∈[ ,3]上恒成立,
,3]上恒成立,
令g(x)=x2-2mx+m2-2m+1,x∈[ ,3],
,3],
只需gmin(x)≥0即可,
而g(x)=(x-m)2-2m+1,x∈[ ,3],
,3],
(1)当m≤ 时,gmin(x)=g(
时,gmin(x)=g( )=
)= -3m+m2+1≥0,
-3m+m2+1≥0,
∴4m2-12m+5≥0,解得m≥ 或m≤
或m≤ ,
,
∴m≤ ;
;
(2)当 <m<3时,gmin(x)=g(m)=-2m+1≥0,解得m≤
<m<3时,gmin(x)=g(m)=-2m+1≥0,解得m≤ 这与
这与 <m<3矛盾;
<m<3矛盾;
(3)当m≥3时,gmin(x)=g(3)=10+m2-8m≥0,解得m≥4+ 或m≤4-
或m≤4- ,
,
而m≥3,
∴m≥4+ ;
;
综上,实数m的取值范围是(-∞, )∪[4+
)∪[4+ ,+∞]。
,+∞]。


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 2 |
| π |
| 4 |
| 7 |
| 5 |
| 7 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
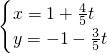 (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为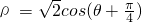 ,则直线l被曲线C所截得的弦长为________.
,则直线l被曲线C所截得的弦长为________.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省赣州市十一县市高三(上)期中数学试卷(理科)(解析版) 题型:填空题
 (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 ,则直线l被曲线C所截得的弦长为 .
,则直线l被曲线C所截得的弦长为 .查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省赣州市十一县市高三(上)期中数学试卷(理科)(解析版) 题型:填空题
 (t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为
(t为参数),若以O为极点,x轴正半轴为极轴建立极坐标系,则曲线C的极坐标方程为 ,则直线l被曲线C所截得的弦长为 .
,则直线l被曲线C所截得的弦长为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com