练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    使等式m2+2m-sinx=0(x∈R）成立的实数m满足的条件是(    )

    A．m＜-2或m＞0     B．-1≤m≤1C．-1-≤m≤-1+   D．全体实数

    C

    解析：sinx=m2+2m，∴-1≤-1≤m2+2m≤1.

    解得-1-≤m-1+.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知复数z=（m2-2m-3）+（m2-3m-4）i，求实数m的值使z为纯虚数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知椭圆C：数学公式+数学公式=1（a＞b＞0）的离心率为数学公式，过右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的中点．
    （1）求直线ON（O为坐标原点）的斜率KON；
    （2）对于椭圆C上任意一点M，试证：总存在角θ（θ∈R）使等式：数学公式=cosθ数学公式+sinθ数学公式成立．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年山东省实验中学高二（下）期末数学试卷（理科）（解析版） 题型：解答题

    已知椭圆C：+=1（a＞b＞0）的离心率为，过右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的中点．
    （1）求直线ON（O为坐标原点）的斜率KON；
    （2）对于椭圆C上任意一点M，试证：总存在角θ（θ∈R）使等式：=cosθ+sinθ成立．

    查看答案和解析>>

    科目：高中数学 来源：2009年高考数学压轴试卷集锦（4）（解析版） 题型：解答题

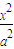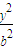    已知椭圆C：+=1（a＞b＞0）的离心率为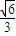，过右焦点F且斜率为1的直线交椭圆C于A，B两点，N为弦AB的中点．
    （1）求直线ON（O为坐标原点）的斜率KON；
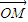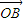    （2）对于椭圆C上任意一点M，试证：总存在角θ（θ∈R）使等式：=cosθ+sinθ成立．

    查看答案和解析>>

    同步练习册答案