
【探究】 (1)设点P、Q的坐标为(x1,y1)、(x2,y2).
由OP⊥OQ得 kOP·kOQ=-1
即![]() .x1x2+y1y2=0. ①
.x1x2+y1y2=0. ①
又(x1,y2),(x2,y2)是方程组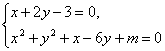 的实数解即x1、x2是方程5x2+10x+4m-27=0的两个根. ②
的实数解即x1、x2是方程5x2+10x+4m-27=0的两个根. ②
∴ x1+x2=-2,x1x2=![]() . ③
. ③
∵ P、Q在直线x+2y-3=0上,
∴ y1y2=![]() (3-x1)·
(3-x1)·![]() (3-x2)=
(3-x2)=![]() [9-3(x1+x2)+x1x2].
[9-3(x1+x2)+x1x2].
将③代入,得 y1y2=![]() . ④
. ④
将③④代入①,解得m=3,代入方程②,检验Δ>0成立,∴m=3.
(2)由直线方程可得3=x+2y,代入圆的方程x2+y2+x-6y+m=0,有x2+y2+![]() (x+2y)(x-6y)+
(x+2y)(x-6y)+![]() (x+2y)2=0,整理得
(x+2y)2=0,整理得
(12+m)x2+4(m-3)xy+(4m-27)y2=0.
由于x≠0,故可得(4m-27)(![]() )2+4(m-3)
)2+4(m-3)![]() +12+m=0.
+12+m=0.
∴ kOP,kOQ是上述方程两根.
由kOP·kOQ=-1,得![]() ,解得m=3.
,解得m=3.
经检验可知m=3为所求.
【规律总结】 求解本题时,应避免去求P、Q两点的坐标的具体数值.除此之外,还应对求出的m值进行必要的检验,这是因为在求解过程中并没有确保有交点P、Q存在.
(1)显示了一种解这类题的通法,(2)的关键在于依据直线方程构造出一个关于![]() 的二元齐次方程,虽有规律可循,但需一定的变形技巧,同时也可看出,这种方法给人以一种酣畅淋漓,一气呵成的感觉.
的二元齐次方程,虽有规律可循,但需一定的变形技巧,同时也可看出,这种方法给人以一种酣畅淋漓,一气呵成的感觉.


科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com