
 =
= ,
, =(cosx-sinx,2sinx),若函数f(x)=
=(cosx-sinx,2sinx),若函数f(x)= •
• .
. =
= ,
, =(cosx-sinx,2sinx)
=(cosx-sinx,2sinx) cosx•2sinx=cos2x+
cosx•2sinx=cos2x+ sin2x=2sin(2x+
sin2x=2sin(2x+ ),(4分)
),(4分) ≤2x+
≤2x+ ≤
≤ ,即
,即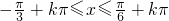 (k∈Z),
(k∈Z), (k∈Z);(6分)
(k∈Z);(6分) )=
)= .
. <2x+
<2x+ <
< ,
, =
= ,∴A=
,∴A= .
. =
=
 (12分)
(12分) ,再利用余弦定理及a=1,b+c=2,即可得到结论.
,再利用余弦定理及a=1,b+c=2,即可得到结论.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
| AB |
| MB |
| BC |
| OM |
| CO |
| AB |
| a |
| b |
| e1 |
| e2 |
| 1 |
| 2 |
| 3 |
| 4 |
| a |
| b |
| a |
| b |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| AP |
| AO |
| AC |
| PA |
| PB |
| PC |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| AB |
| MB |
| BC |
| OM |
| CO |
| AB |
| a |
| b |
| e1 |
| e2 |
| 1 |
| 2 |
| 3 |
| 4 |
| a |
| b |
| a |
| b |
| a |
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)已知向量![]() ,
,![]() ,其中
,其中![]() ,且
,且![]() ,又函数
,又函数![]() 的图象任意两相邻对称轴间距为
的图象任意两相邻对称轴间距为![]() . w ww.ks 5u.co m
. w ww.ks 5u.co m
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设![]() 是第一象限角,且
是第一象限角,且![]() ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分14分)已知向量![]() ,
,![]() ,其中
,其中![]() ,且
,且![]() ,又函数
,又函数![]() 的图象任意两相邻对称轴间距为
的图象任意两相邻对称轴间距为![]() . w ww.ks 5u.co m
. w ww.ks 5u.co m
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设![]() 是第一象限角,且
是第一象限角,且![]() ,求
,求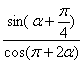 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com